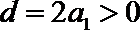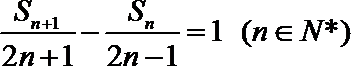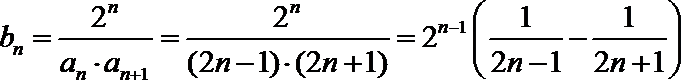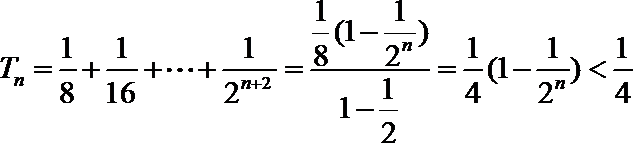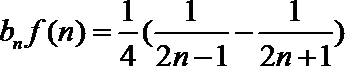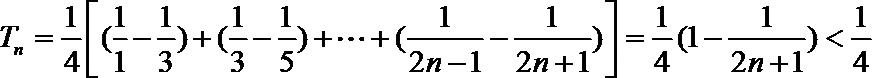- 由数列的前几项求通项
- 共778题
2.行列式

正确答案
11
解析
解析已在路上飞奔,马上就到!
知识点
23.已知数列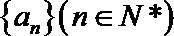
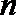
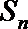
(1)当数列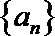
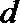
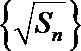
(2)若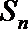
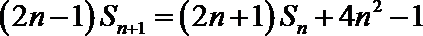
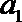
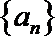
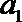
(3)若数列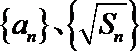
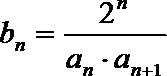
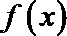
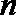
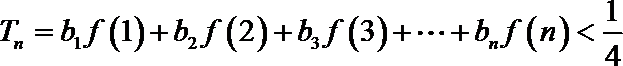
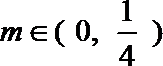
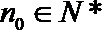
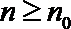
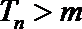
正确答案
(1)数列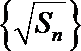
(2)∵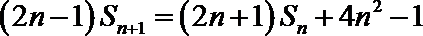
∴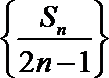
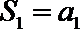
∴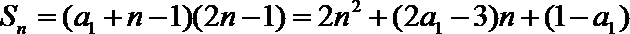
当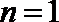
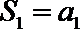
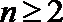
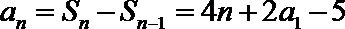
∵数列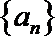
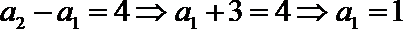
∴存在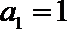
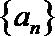
(3)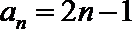
构造①:令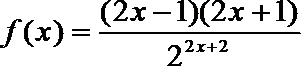
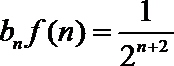
若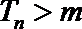
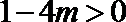
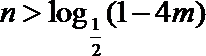
∴令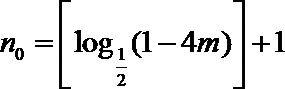
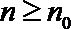
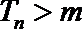
构造②:令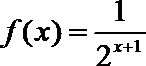
若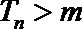
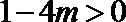
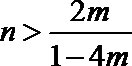
∴令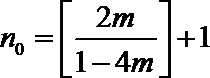
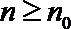
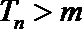
解析
解析已在路上飞奔,马上就到!
知识点
15.数列
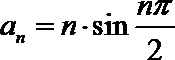


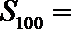
正确答案
-50
解析
解析已在路上飞奔,马上就到!
知识点
23.已知以a为首项的数列
(1)若0<

(2)若a,k∈N﹡,求使
(3)若

正确答案
(1)当



故


(2)①当


同理可得,当

当

②当

③当
综上得:当

当

(3)由m


当

故


所以
故
=4
=
解析
解析已在路上飞奔,马上就到!
知识点
14.设数列








正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.定义:如果一个向量列从第二项起,每一项与它的前一项的差都等于同一个常向量,那么这个向量列叫做等差向量列,这个常向量叫做等差向量列的公差.
已知向量列





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.在等差数列



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.正项无穷等比数列


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.观察如图类似杨辉三角的数表,则此表最后一个数是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.已知等差数列
(1)求数列
(2)设各项均为正数的等比数列

正确答案
(1)设等差数列
∴数列
(2)设各项均为正数的等比数列
由(1)知

解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析