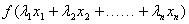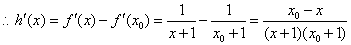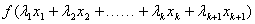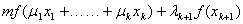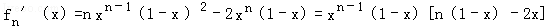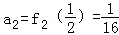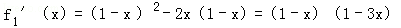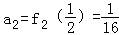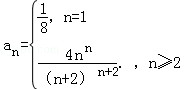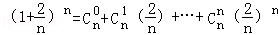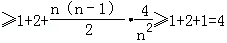- 由数列的前几项求通项
- 共778题
公差不为零的等差数列







正确答案
60
解析
略
知识点
已知函数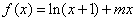
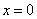
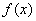
(1)求实数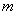
(2)已知结论:若函数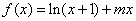
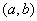
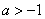
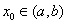
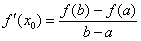
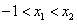
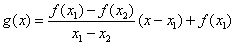
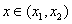
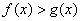
(3)已知正数

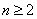
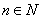
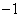
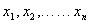
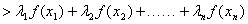
正确答案
见解析。
解析
(1)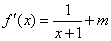


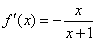
当

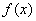
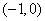
当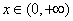
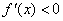

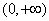

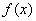
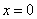
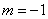
(2)令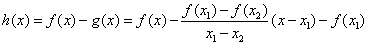
则
∵函数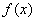
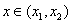

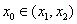
使得
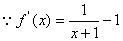
∵当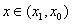
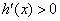
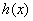
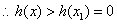
∵当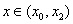
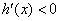
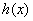
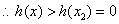
故对任意
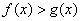
(3)用数学归纳法证明。
①当
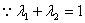
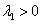

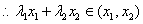

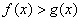
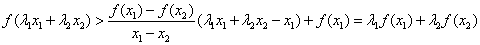

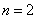
②假设当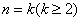
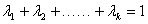
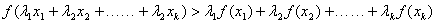
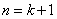
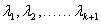
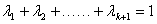
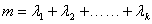

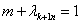
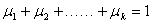
>
>
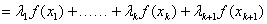

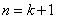
综上由①②,对任意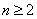
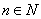
知识点
数列



(1)若数列
(2)设


(3)设各项均不为0的数列





正确答案
见解析。
解析
(1)由题意,当

两式相减,得
所以,当



则只需

(2)由(1)得,等比数列


∴
∴
上式两边乘以3得
①-②得
∴
(3) 由(2)知
∵

∵
∴数列
由

∴数列
知识点
设函数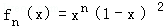
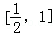
(1)求a1,a2的值;
(2)求数列{an}的通项公式;
(3)证明:对任意n∈N*(n≥2),都有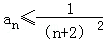
正确答案
见解析。
解析
(1)解法1:∵
当n=1时,f1'(x)=(1﹣x)(1﹣3x)
当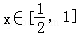
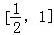
∴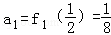
当n=2时,f2'(x)=2x(1﹣x)(1﹣2x)
当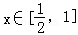
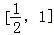
∴
解法2:当n=1时,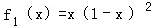
当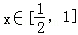
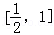
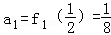
当n=2时,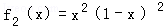
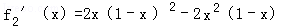
当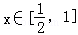
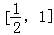
∴
(2)令fn'(x)=0得x=1或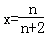
∵当n≥3时,
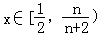
当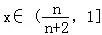
故fn(x)在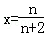
即当n≥3时,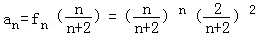
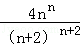
当n=2时(*)仍然成立,
综上得
(3)当n≥2时,要证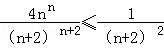
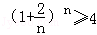
∵
∴对任意n∈N*(n≥2),都有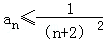
知识点
设实数


正确答案
解析
略
知识点
扫码查看完整答案与解析