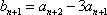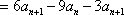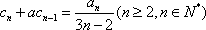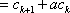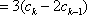- 由数列的前几项求通项
- 共778题
已知等比数列






(1)求数列




正确答案
见解析
解析
解:(1)设数列

若






由



即

(2)由(1)得,
所以
知识点
已知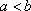
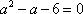
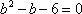
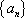
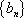
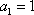
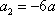
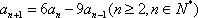
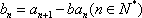
(1) 求证数列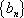
(2) (理科)求数列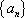
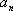
(3) (理科)若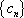
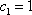
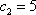
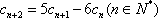
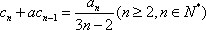
正确答案
见解析
解析
(1)∵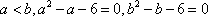
∴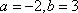
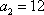
∵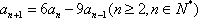
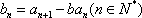
∴
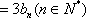
又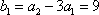
∴数列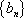
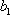
(2)依据(1)可以,得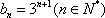
于是,有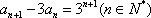
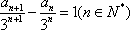
因此,数列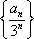
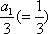
故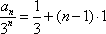
所以数列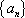
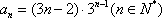
(3)用数学归纳法证明:
(i)当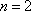
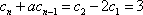
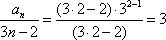
即左边=右边,所以当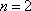
(ii)假设当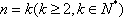
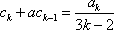
当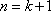
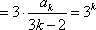
右边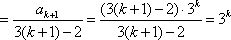
即左边=右边,因此,当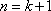
根据(i)、(ii)可以断定,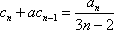
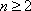
所以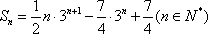
知识点
在平面直角坐标系上,设不等式组



(1)求数列
(2)若



正确答案
见解析。
解析
(1)由

所以平面区域为

直线



(2)由

知识点
已知函数









(1)若k=1,求数列
(2)若m=2,问是否存在常数


(3)若

正确答案
见解析
解析
解析:(1)因为
所以其值域为
于是
又
(2)因为
所以
法一:假设存在常数
使得数列
得
法二:假设存在常数k>0,使得数列


当
则
(3)因为


于是
则

因此

又

进而有
知识点
在数列

(1)数列


(2)数列


正确答案
(1)
解析
法1:
法2:
(1)
(2)
知识点
扫码查看完整答案与解析