- 由数列的前几项求通项
- 共778题
对大于或等于2的正整数的幂运算有如下分解方式:
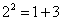
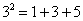
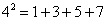
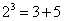
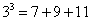
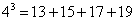
根据上述分解规律,若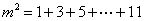
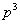
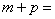
正确答案
11
解析
由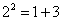
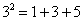
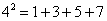
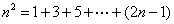
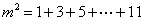
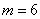
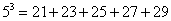
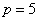
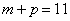
知识点
已知数列






(1)求数列

(2)若


正确答案
见解析。
解析
(1)由题意得
当

又
设等差数列



可得

所以

(2)由(1)得,当



所以当

当

记

①-②得
故
则
因为

知识点
在数列


(1) 求

(2)设


正确答案
见解析。
解析
(1)容易求得:
故可以猜想

(i) 显然当
(ii) 假设当



那么当
即当


(2)
所以
所以只需要证明

所以对任意的自然数
知识点
已知数列








(1)求数列

(2)令数列




正确答案
见解析。
解析
(1)由已知可知数列
∴数列

∵



又



(2)由已知得:
∴
∴
∴两式相减得

∴数列


知识点
某学校某班文娱小组的每位组员唱歌、跳舞至少会一项,已知已知会唱歌的有2人,会跳舞听有5人,现从中选2人。设

(1)请你判断该班文娱小组的人数并说明理由;
(2)求
正确答案
见解析。
解析
解法一:(1)设既会唱歌又会跳舞的有x人,那么由题意可知:
只会唱歌的有(2-x)人,只会跳舞的有(5-x)人,
文娱队中共有(7-x)人,那么只会一项的人数是(7-2 x)人。
显然x可以取得的值只有0,1,2
① 当x=0时,
② 当x=1时,
所以x=1时不符合题意
③当x=2时,
综上可知道:既会唱歌又会跳舞的有2人,且文娱队中共有5人
(2)


∴

解法二:设既会唱歌又会跳舞的有x人,则文娱队中共有(7-x)人,那么只会一项的人数是(7-2 x)人。
(1)∵

即

故文娱队共有5人,
(2) 


∴

知识点
扫码查看完整答案与解析



























