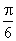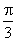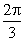弧度与角度的互化
共37题

· 弧度与角度的互化

弧度与角度的互化
共37题

热门试卷

X 查看更多试卷

题型：单选题

单选题 · 5 分

9.在中，的平分线交于，则的长为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

弧度与角度的互化

题型：单选题

单选题 · 5 分

已知平面向量，满足，，则与的夹角为（）

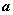
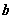
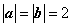
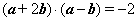
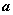
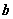
正确答案

解析

略

知识点

弧度与角度的互化

题型：填空题

填空题 · 5 分

在极坐标系中，已知点A（1，），点P是曲线ρsin2θ=4cosθ上任意一点，设点P到直线ρcosθ+1=0的距离为d，则丨PA丨+d的最小值为　　。

正确答案

解析

点A（1，）的直角坐标为A（0，1），

曲线曲线ρsin2θ=4cosθ的普通方程为y2=4x，是抛物线。

直线ρcosθ+1=0的直角坐标方程为x+1=0，是准线。

由抛物线定义，点P到抛物线准线的距离等于它到焦点A（0，1）的距离，

所以当A，P，F三点共线时，其和最小，

最小为|AF|=，

故答案为：。

知识点

弧度与角度的互化

题型：填空题

填空题 · 4 分

若 .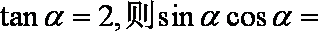

正确答案

解析

知识点

弧度与角度的互化

题型：简答题

简答题 · 10 分

在极坐标系中，点O(0,0)，。

（1）求以为直径的圆的直角坐标方程；

（2）若直线的极坐标方程为，判断直线与圆的位置关系。

正确答案

见解析

解析

（1）设P(ρ，θ)是所求圆上的任意一点，因为为直径，所以，

则

亦即，

故所求的圆的直角坐标方程为

（2）圆的圆心的坐标为，半径为，直线的直角坐标方程为

因为圆心到直线距离为，所以直线与圆相切

知识点

弧度与角度的互化

题型：单选题

单选题 · 5 分

已知一个空间几何体的三视图如图所示，且这个空间几何体的所有顶点都在一个球面上，则这个球的体积是( )

正确答案

解析

略

知识点

弧度与角度的互化

题型：简答题

简答题 · 10 分

已知椭圆（）的左，右焦点分别为，上顶点为。为抛物线的焦点，且，0。

（1）求椭圆的标准方程；

（2）过定点的直线与椭圆交于两点（在之间），设直线

的斜率为（），在轴上是否存在点，使得以为邻边的平行四边形为菱形？若存在，求出实数的取值范围；若不存在，请说明理由。

正确答案

见解析

解析

解：

（1）由已知，，，所以，

在中，为线段的中点，

故，所以，

于是椭圆的标准方程为

（2）设（），

，取的中点为。

假设存在点使得以为邻边的平行四边形为菱形，则。

，

，又，所以，

因为，所以，，

因为，所以，即，

整理得，

因为时，，，所以，

知识点

弧度与角度的互化

题型：单选题

单选题 · 5 分

集合，，若，则实数的值为

A3或-3

C3或-1

D-1

正确答案

解析

略

知识点

弧度与角度的互化

题型：简答题

简答题 · 12 分

21．已知函数f(x) =x2-ax-aln(x-1) (a∈R)。

（Ⅰ）求函数f(x)的单调区间；

（Ⅱ）试说明是否存在实数a(a≥1)，使y= f(x)的图象与直线y=1+ln无公共点。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

弧度与角度的互化

题型：单选题

单选题 · 6 分

9.对于定义域为R的函数，给出下列命题：

①如果函数对任意的，都有（为一个常数），那么函数必为偶函数；

②如果函数对任意的，满足，那么函数是周期函数；

③如果函数对任意的且，都有，那么函数在上是增函数；

④函数和函数的图象一定不能重合.

其中，真命题的个数是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

弧度与角度的互化

继续学习学习下一知识点

下一知识点 : 弧度制的应用

百度题库 > 高考 > 理科数学 > 弧度与角度的互化

扫码查看完整答案与解析