- 等差数列与等比数列的综合
- 共59题
20.已知等比数列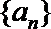
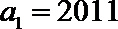

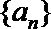
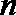
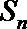
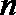
(1)证明: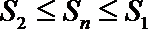
(2)判断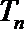
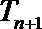
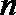
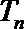
(3)证明:若数列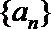
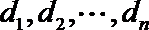
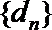
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.等差数列



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.已知数列{an}满足a1=1,an=logn(n+1)(n≥2,n∈N*).定义:使乘积a1·a2·…·ak为正整数的k(k∈N)叫作“酷数”.则在[1,2016]内所有“酷数”的和为( ).
正确答案
解析
∵an=logn(n+1),∴a1·a2·a3·…·an=1×log23×log34×…×logn(n+1)=




则在[1,2016]内所有“酷数”的和为21-1+22-1+…+210-1=
知识点
已知等差数列{an}的公差不为零,a1=25,且a1,a11,a13成等比数列.
18.求{an}的通项公式;
19.求a1+a4+a7+…+a3n-2.
正确答案
an=-2n+27,(2)Sn=(a1+a3n-2)=·(-6n+56)=-3n2+28n.
解析
解: (1)设{an}的公差为d.由题意,a=a1a13,[即(a1+10d)2=a1(a1+12d), 于是d(2a1+25d)=0.又a1=25,所以d=0(舍去),或d=-2.故an=-2n+27
考查方向
解题思路
本题考查等差数列和等比数列,数列的求和,解题步骤如下:设出等差数列的公差,由已知等比数列构造出一个方程解出符合题意的公差,写出数列的通项公式。
易错点
求和的时候将里面的项数弄错,等比中项性质。
正确答案
Sn=(a1+a3n-2)=·(-6n+56)=-3n2+28n.
解析
令Sn=a1+a4+a7+…+a3n-2.由(1)知a3n-2=-6n+31, 故{a3n-2}是首项为25,公差为-6的等差数列.
从而Sn=(a1+a3n-2)=·(-6n+56)=-3n2+28n.
考查方向
解题思路
要求的数列也是一个等差数列,利用等差数列的前n项和公式解答即可。
易错点
求和的时候将里面的项数弄错,等比中项性质。
6.已知等差数列



正确答案
2
解析
设







考查方向
解题思路
本题考查运用等差数列及等比数列性质求首项,解题步骤如下:设







易错点
本题必须注意审题,忽视则会出现错误。
知识点
扫码查看完整答案与解析