- 二次函数的应用
- 共461题
1
题型:填空题
|
设
正确答案
解析
设


知识点
二次函数的应用
1
题型:简答题
|
如图,锐角









正确答案
见解析。
解析
由圆



因为





所以
又
所以
由

知识点
二次函数的应用
1
题型:简答题
|
在数列中,



(1)求


(2)设




正确答案
见解析
解析
(1)容易求得:

故可以猜想

(i) 显然当
(ii) 假设当




那么当
------------(6分)
即当


(2)
所以
-----------------------(11分)
所以只需要证明

所以对任意的自然数

知识点
二次函数的应用
1
题型:
单选题
|
设曲线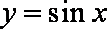
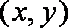
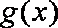
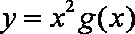
正确答案
C
解析
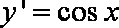
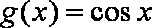
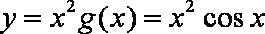
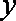
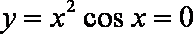
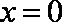
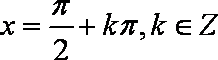
知识点
二次函数的应用
1
题型:简答题
|
已知

正确答案
见解析。
解析
证法一:因为


所以
故
又3
所以原不等式成立,
证法二:因为



所以
同理
故
所以原不等式成立。
知识点
二次函数的应用
下一知识点 : 幂函数的概念、解析式、定义域、值域
扫码查看完整答案与解析