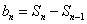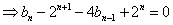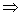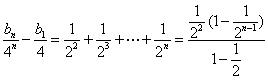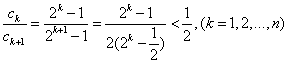- 由an与Sn的关系求通项an
- 共102题
1
题型:
单选题
|
在数列


正确答案
B
解析
略
知识点
由an与Sn的关系求通项an
1
题型:简答题
|
已知等比数列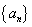
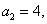
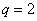
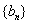
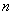
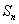
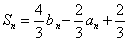

(1)求数列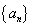
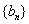
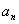
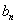
(2)设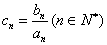
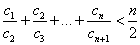
正确答案
见解析。
解析
(1) 解法一:由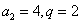
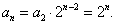
由上式结合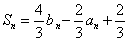
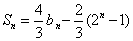
则当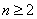
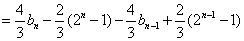
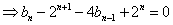
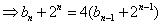
∵
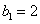
∴数列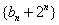
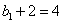
∴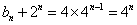
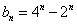
【解法二:由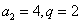
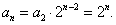
由上式结合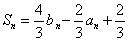
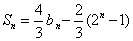
则当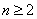
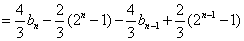
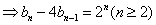
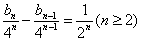
∴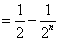
∵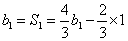
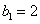
∴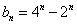
(2) 由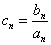
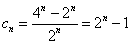
【或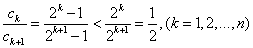
∴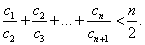
知识点
由an与Sn的关系求通项an等比数列的性质及应用数列与不等式的综合
1
题型:简答题
|
已知








(1)求数列


(2)设数列




正确答案
见解析。
解析
(1)设数列

由已知得


∴ 
得
∵ 已知
∴ 
∴ 
(2)由(1)知
而等比数列

∴
因此
∵
∴
∴
∵当
∴ 
∴
∴当

当
综上得不等式
法二∵当
∴ 
∴ 
∴当

当

当
综上得不等式
(法三) 利用二项式定理或数学归纳法可得:
所以,




知识点
由an与Sn的关系求通项an
1
题型:
单选题
|
在数列


正确答案
B
解析
略
知识点
由an与Sn的关系求通项an
1
题型:填空题
|
已知数列






正确答案

解析
略
知识点
由an与Sn的关系求通项an其它方法求和
下一知识点 : 由递推关系式求数列的通项公式
扫码查看完整答案与解析