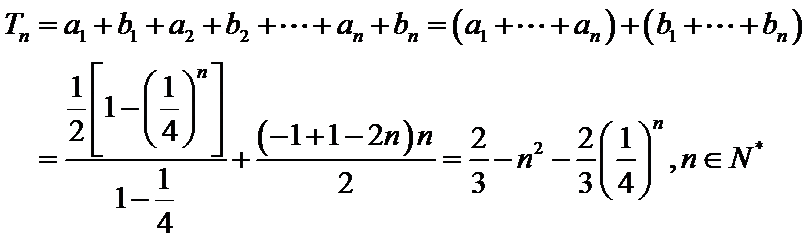- 由an与Sn的关系求通项an
- 共102题
17. 已知数列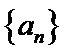

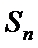
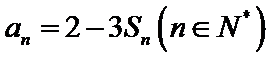
(I)求数列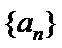
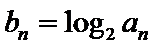
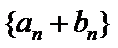
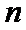

正确答案
(1)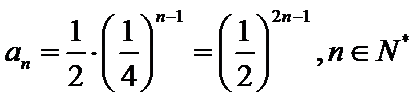
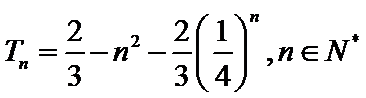
解析
试题分析:本题属于数列求通项公式和数列求和的基本问题,题目的难度是逐渐由易到难,(1)确定数列的首项和公比.(2)将两个数列分别求和之后再相加.(3)正项等比数列取对数以后的数列为等差数列.
(Ⅰ)当
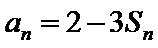
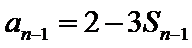
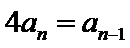
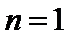
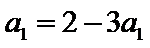
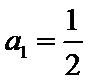
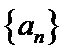
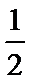
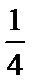

(Ⅱ)由(Ⅰ)知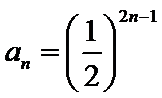
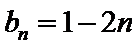
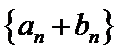
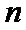
考查方向
解题思路
本题考查等差数列和等比数列及分组求和法、简单对数值的求法. 1、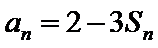
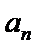
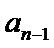
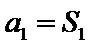
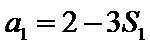
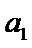
易错点
第一问中容易少去对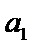
知识点
16.已知各项均为正数的数列







正确答案

解析
由已知,

所以
因为


所以,数列


所以






考查方向
解题思路
本题主要考查数列及等差数列的概念和性质,
解题步骤如下:用

由
易错点
本题不易想到用
知识点
20.若数列

(1)已知数列

①求数列
②试判断数列
(2)已知数列


正确答案
(1)①
(2)略.
解析
试题分析:此题是结合等差(比)数列,给出新定义的创新试题,难度较大。在解题中要充分利用新定义的性质,合理推理,得出结论。
(1)①由an+1=2an-1,得an+1-1=2(an-1),且a1-1=1,
所以数列{an-1}是首项为1,公比为2的等比数列.
所以an-1=2n-1.
所以,数列{an}的通项公式为a n=2n-1+1.
②数列{an}不是“等比源数列”.用反证法证明如下:
假设数列{an}是“等比源数列”,则存在三项am,an,ak (m<n<k)按一定次序排列构成等比数列.
因为an=2n-1+1,所以am<an<ak.
所以an2=am·ak,得 (2n-1+1)2=(2m-1+1)(2k-1+1),即22n-m-1+2n-m+1-2k-1-2k-m=1.
又m<n<k,m,n,k∈N*,
所以2n-m-1≥1,n-m+1≥1,k-1≥1,k-m≥1.
所以22n-m-1+2n-m+1-2k-1-2k-m为偶数,与22n-m-1+2n-m+1-2k-1-2k-m=1矛盾.
所以,数列{an}中不存在任何三项,按一定次序排列构成等比数列.
综上可得,数列{an}不是“等比源数列”.
(2)不妨设等差数列{an}的公差d≥0.
当d=0时,等差数列{an}为非零常数数列,数列{an}为“等比源数列”.
当d>0时,因为an∈Z,则d≥1,且d∈Z,所以数列{an}中必有一项am>0.
为了使得{an}为“等比源数列”,
只需要{an}中存在第n项,第k项(m<n<k),使得an2=amak成立,
即[am+(n-m)d]2=am[am+(k-m)d],即(n-m)[2am+(n-m)d]=am(k-m)成立.
当n=am+m,k=2am+amd+m时,上式
所以,数列{an}为“等比源数列”.
考查方向
解题思路
本题主要考查数列的概念、等差数列、等比数列的的通项公式与求和公式、不等式的求解等基本性质.
解题步骤如下:
根据已知条件构造新数列,从而求出数列的通项a n;利用等差(比)数列的性质,和题目给出的新定义“等比源数列”进行合理的恒等变换和推理,得出解答。
易错点
不能正确理解题目中给出的新定义“等比源数列”
在判断“等比源数列”中的恒等变换时易出错。
知识点
16.已知数列






正确答案
解析

当

由①-②得到, 
(1)当

化简得
所以当n为奇数时,
(2)当

即

带入得到
所以当n为偶数时
所以
当n为奇数时,

所以
即
当n为偶数时,

所以
即
综上得实数

考查方向
解题思路
1.先根据
2.对于递推公式分奇数、偶数讨论后求出通项公式,然后带入
易错点
1.对于

2.对于
知识点
16.设数列



正确答案
解析
当

即


由题意得:

①-②得:

∵




∴
故此题答案为
考查方向
本题主要考查等差数列的基本运算与性质,意在考查考生的运算求解能力及通项求和公式的综合应用,在近几年的各省高考题中出现的频率较高。
解题思路
1、先根据


2、再要根据
易错点
1、本题易出现的问题是由

2、本题易忽视数列
知识点
扫码查看完整答案与解析