- 直线和圆的方程
- 共1449题
已知直线





正确答案
解析
圆心O到直线





知识点
如图,在四棱锥








(1)求证:平面

(2)若二面角


正确答案
见解析。
解析
(1)∵PA⊥平面ABCD, BC平面ABCD,∴PA⊥BC,
又AB⊥BC,PA∩AB=A, ∴BC⊥平面PAB,
∵BC
(2)以A为原点,AB为x轴、AP为z轴,建立如图所示的空间直角坐标系A—xyz。
则B(2,0,0),C(2,1,0),D(1,1,0)。
设P(0,0,a)(a>0),
则



设n1=(x1,y1,z1)为面BPC的一个法向量,
则n1·

即
取x1=a,y1=0,z1=2,得n1=(a,0,2)。
同理,n2=(0,a,1)为面DPC的一个法向量。 ……………………………10分
依题意,
解得a2=2,或a2=-7(舍去),所以

知识点
斜率为k(k≠0)的两条直线分别切函数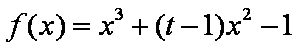
正确答案
解析
略
知识点
已知直线



正确答案
3x+4y-1=0或3x+4y+9=0
解析
设直线






知识点
如图,直四棱柱ABCD-A1B1C1D1底面ABCD为菱形,AB=1 AA1= 

(1)求证:BD1丄平面AB1C;
(2)在棱A1D1上是否存在一点E,使得二面角B1-AC-E的大小为60°?若存在,求出A1E的长;若不存在,说明理由。
正确答案
见解析。
解析
(1) 取



以







则




从而


则



所以

(2)假设这样的点


由(1)可知,

由



令二面角





满足点




知识点
在平面直角坐标系




若圆






正确答案
解析
略
知识点
如图所示,PA为⊙O的切线,A为切点,PBC是过点O 的割线,



(1)求证:
(2)求
正确答案
见解析。
解析
(1)∵


又



(2)∵




又∵



由(1)知,


∴


连结




∴

知识点
在三棱锥







(1)证明:
(2)求
正确答案
见解析
解析
(1)取










则
所以
故

(2)由(1)知,

则得平面
则

知识点
如图,角α的始边与x轴的非负半轴重合,终边与单位圆交于点A (x1,yl),将射线OA按逆时针方向旋转
(1)若角α为锐角,求f(α)的取值范围;
(2)比较f(2)与f(3)的大小。
正确答案
见解析。
解析
(1)∠AOB=

f(α)=xl﹣x2 =cosα﹣cos(α+




=

∵角α为锐角,∴




∴





(2)∵f(2)=









∴f(2)>f(3)。
知识点
已知ABC是边长为3的等边三角形,点D、E分别是边AB、AC上的点,且满足==.将ADE沿DE折起到1ADE的位置,并使得平面A1DE⊥平面BCED.
(1)求证:A1D⊥EC;
(2)设P为线段BC上的一点,试求直线PA1与平面A1BD所成角的正切的最大值。
正确答案
见解析
解析
解析:(1)因为等边△

所以



由余弦定理得
因为
所以
折叠

因为平面







故A1D⊥EC.…………6分
(2)法一:由(1)的证明,可知


以
















所以


所以
因为



设直线


所以
①若


②若
令
因为函数

即
所以
故所求的最大值为
法二:如图,作



由(1)有



所以


所以


设


所以A1H=
所以在


①若x=0,则tan


②若

令
因为函数

所以tan

知识点
由曲线
正确答案
解析
围成的图形如图,面积为
知识点
如图,











正确答案
解析
由题知,










知识点
已知






(1)求
(2)当


正确答案
见解析
解析
(1)因为
即

所以 
(2)由
故
由


由正弦定理,
故
知识点
如图,已知抛物线










(1)求抛物线
(2)当


(3)若直线



正确答案
(1)

解析
解析:(1)∵点

∴


(2)法一:∵当



设

∴

∴

法二:∵当







联立方程组

∵


同理可得


(3)法一:设


可得,直线

同理,直线

∴

∴直线



∵



法二:设点


以


⊙

①-②得:直线

当



∵



知识点
在极坐标系中,圆








正确答案
解析
将圆













知识点
扫码查看完整答案与解析


















































