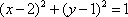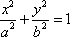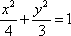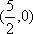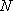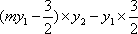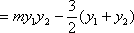- 直线和圆的方程
- 共1449题
3. 




正确答案
解析
知识点
已知圆C:(x+1)2+(y-3)2=9上的两点P,Q关于直线x+my+4=0对称,那么m=_________.
正确答案
-1
解析
略
知识点
在圆







正确答案
解析
过点

















知识点
圆
正确答案
1
解析
在直角坐标系下的圆的方程为

知识点
已知圆的直角坐标方程为

正确答案
解析
略
知识点
已知圆的方程为


正确答案
解析
略
知识点
设数列
(1)求
(2)设


正确答案
见解析。
解析
(1)由
数列
故
(2)

知识点
当圆


正确答案
0
解析
略
知识点
若圆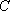
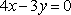

正确答案
解析
略
知识点
4.已知椭圆

正确答案
解析
因为与直线
考查方向
本题主要考查点到直线的距离,这类试题常和圆锥曲线相关知识一起考查。
解题思路
数形结合,先画出椭圆的大致形状和直线的位置,有且仅有一点的距离为1,找到一条直线与这个椭圆相切的直线。带入方程即可。
易错点
椭圆方程的各种形式的转化,点到直线的距离公式理解不透彻
知识点
已知以原点为对称中心、F(2,0)为右焦点的椭圆C过P(2,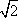
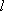
(1)求椭圆C的方程;
(2)是否存在实数k,使线段AB的垂直平分线经过点Q(0,3)?若存在求出 k的取值范围;若不存在,请说明理由。
正确答案
见解析
解析
(1)设椭圆C的方程为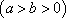
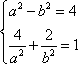
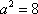
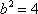
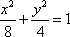
(2)假设存在斜率为k的直线,其垂直平分线经过点Q(0,3),
设A(x1,y1)、B(x2,y2),AB的中点为N(x0,y0),
由
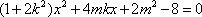
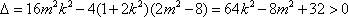
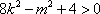
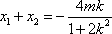
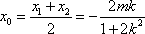
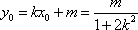

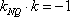
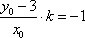
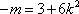
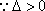
整理得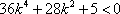

知识点
如图,圆







正确答案
4,
解析
略
知识点
已知动点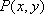
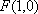
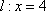

(1)求动点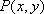
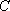
(2)已知直线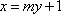
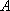
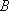
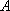
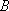
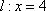
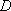
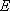
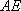
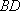
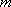
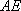
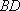
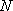
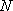
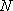
正确答案
(1)
(2)直线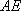
解析
(1)由题意得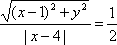
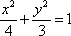
所以动点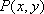
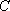
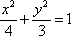
(2)当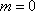
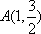
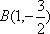
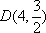
直线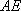
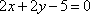
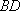
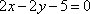
方程联立解得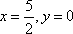
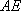
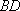
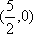
假设直线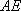
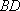
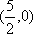
证明:设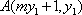
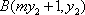
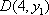
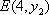
由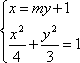

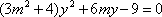
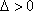
由韦达定理得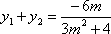
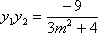
因为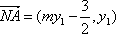
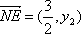
所以
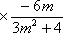
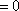
所以,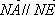
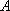
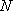
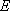
同理可证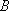
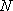
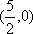
知识点
已知正三角形内切圆的半径是高的
正确答案
解析
略
知识点
经过点F (0,1)且与直线y=﹣1相切的动圆的圆心轨迹为M点A、D在轨迹M上,且关于y轴对称,过线段AD (两端点除外)上的任意一点作直线l,使直线l与轨迹M 在点D处的切线平行,设直线l与轨迹M交于点B、C。
(1)求轨迹M的方程;
(2)证明:∠BAD=∠CAD;
(3)若点D到直线AB的距离等于
正确答案
见解析。
解析
(1)设圆心坐标为(x,y),由题意动圆经过定点F(0,1),且与定直线:y=﹣1相切,
所以 
即(y﹣1)2+x2=(y+1)2,
即x2=4y,故轨迹M的方程为x2=4y。
(2)由(1)得y=

设D(x0,

则A(﹣x0,


则kBC=


kAC=


∴kBC+AB=


∴∠BAD=∠CAD。
(3)点D到直线AB的距离等于
不妨设C在AD上方,即x2<x1,直线AB的方程为:y﹣
解得B点的坐标为(x0﹣4,


由(2)知,∠CAD=∠BAD=45°,同理可得|AC|=2
∴△ABC的面积为


解得x0=±3。
当x0=3时,B((﹣1,

当x0=﹣3时,B((﹣7,

知识点
扫码查看完整答案与解析