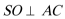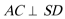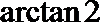- 棱柱、棱锥、棱台的体积
- 共114题
14.在三棱柱
正确答案
解析
本题主要考查了三棱柱的体积的求解，解题步骤如下：
考查方向
本题主要考查了三棱柱的体积/几何体的体积计算是高考中的热点，主要涉及有三视图求体积、顶点转换法求三棱锥的体积，属于中档题。
易错点
不能将三棱柱正确的分割为几个可以求体积的几何体。
知识点
9.已知A,B是球O的球面上两点，∠AOB=90,C为该球面上的动点，若三棱锥O-ABC体积的最大值为36，则球O的表面积为
A
B64π
C144π
D256π
正确答案
知识点
8．已知某几何体的三视图的侧视图是一个正三角形，如图所示，则该几何体的
体积等于
A
B
C
D
正确答案
解析
还原成的几何体如图所示，利用体积计算公式计算，所以选C
考查方向
三视图与几何体的体积
解题思路
利用三视图尺寸还原成立体图形，利用立体图形体积公式求解。
易错点
立体感不强，三视图尺寸理解错误
知识点
11．若一个四棱锥底面为正方形，顶点在底面的射影为正方形的中心，且该四棱锥的体积为9，当其外接球表面积最小时，它的高为
A
B
C
D
正确答案
解析
我们应该掌握一些特殊的多面体与外接球的特征．正四面体外接球的球在其高上，且把高分成
考查方向
本题考查多面体及其外接球问题.正四棱锥与外接球
解题思路
找到高和外接球半径的关系，利用基本不等式求解。
易错点
找不到关系和不会利用基本不等式
知识点
3. 某四棱锥的三视图如图所示，该四棱锥的体积是（ ）
A32
B
C48
D
正确答案
解析
考查方向
本题考查了三视图的概念，锥体的体积公式，及识图能力。
解题思路
（1）正确判断出此正四棱锥的底面边长是4，高是2。
（2）利用锥体体积公式计算，即可得结果。
易错点
（1）不能正确识别此四棱锥是一个底面边长为4，高为2的正四棱锥。
（2）锥体体积公式记错，导致答案错误。
知识点
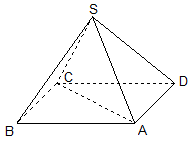
19．如图，某人打算做一个正四棱锥形的金字塔模型，先用木料搭边框，再用其他材料填充。已知金字塔的每一条棱和边都相等。
（1） 求证：直线
（2）若搭边框共使用木料24米，则需要多少立方米的填充材料才能将整个金字塔内部填满？
正确答案
（1）略；
（2）
解析
（1）如图，连接
在正方形
在
（2）边长为3米
解直角三角形SOB，得棱锥的高
答：需要
考查方向
解题思路
1、空间关系的判断与证明通常需要直线与直线，直线与平面，平面与平面三种关系相互转换，本题可以先把线线关系转化为线面关系，再转为线线关系求证。
2、解决正棱锥有关问题通常要研究底边，侧棱，高，斜高，底面外接圆半径，内切圆半径组成的四个直角三角形。本题可以由侧棱，底面外接圆半径和高组成的直角三角形入手求解。
易错点
注意搭建正四棱锥不仅有四条侧棱，含有四条底边。
知识点
5．已知某几何体的三视图如图所示，则该几何体的体积为（ ）
A
B
C
D
正确答案
解析
由三视图判断知此为四棱锥
考查方向
本题主要考查了由三视图还原成实物图再进行体积与表面积的计算，在近几年的各省高考题出现的频率较高，常是独立命题，求体积、表面积与棱长，也与函数结合求最值问题。
易错点
1、无法由三视图还原出实物直观图。
2、公式不熟悉导致出错。
知识点
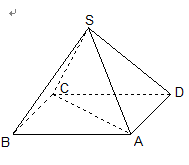
19． 如图，某人打算做一个正四棱锥形的金字塔模型，先用木料搭边框，再用其他材料填充．已知金字塔的每一条棱和边都相等．
（1）求证：直线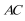
（2）若搭边框共使用木料24米，则需要多少立方米的填充材料才能将整个金字塔内部填满？
正确答案
（1）略；
（2）需要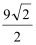
解析
（1）如图，
连接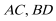
则
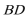
在正方形
对角线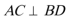
在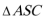
∴
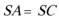
又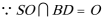
∴
∴
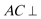
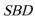
（2）边长为3米，
棱锥的底面积为
棱锥的高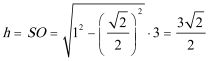
∴
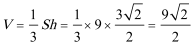
答：需要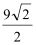
考查方向
本题主要考查立体几何中两直线相互垂直的判定以及简单多面体的体积公式，考查逻辑推理能力以及计算能力．
解题思路
题（1）的证明，先由线面垂直的判定定理证得线面垂直，再由线面垂直的性质定理证得线线垂直．
题（2）的求解，先求得四棱锥的底面积以及高，然后利用四棱锥的体积公式求解即得．
易错点
线线垂直与线面垂直的相互转化，条件缺一不可．题（1）的证明，在证明线面垂直时，必须是平面外的直线分别垂直于平面上的两条相交直线，才能得到线面垂直．
知识点
在三棱锥
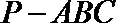
正确答案
解：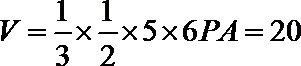
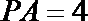
取PC的中点为D，连结AD，DQ，
则
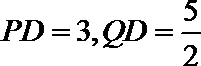
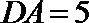
因为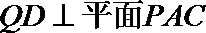
所以
所以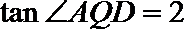
直线PB，AQ所成的角为
解析
本题属于空间几何体的基本问题，题目的难度是简单，本题的关键是通过添加辅助线找出异面直线PB，AQ所成的角,
考查方向
本题考查了空间几何体的体积与异面直线的综合应用
易错点
1、找异面直线PB，AQ所成的角容易出错
知识点
9．图是一个四面体的三视图，这三个视图均是腰长为2的等腰直角三角形，正视图和俯视图中的虚线是三角形的中线，则该四面体的体积为
A
B
C
D2
正确答案
解析
由图可知，此几何体为底边长分别为1，2，高为2的三棱锥。B选项不正确，C选项不正确，D选项不正确，所以选A选项。
考查方向
本题主要考查三视图
解题思路
1、还原几何体；
2、求出体积，即可得到结果。B选项不正确，C选项不正确，D选项不正确，所以选A选项。
易错点
本题易在还原几何体时发生错误。
知识点
扫码查看完整答案与解析