- 并集及其运算
- 共67题
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
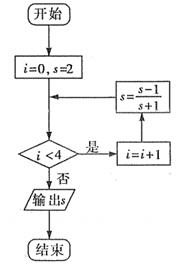
执行如图所示的程序框图,输出的s值为( )。
正确答案
解析
循环操作4次时S的值分别为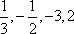
知识点
由直线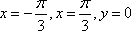
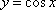
正确答案
解析
由定积分知识可得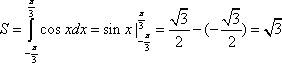
知识点
椭圆




(1)求

(2)设




(i)证明:
(ii)记△MAB,△MDE的面积分别是



请说明理由。
正确答案
见解析
解析
(1)由题意知



故


(2)(1)由题意知,直线



由

设


又点

故

(2)设直线的斜率为




又直线


于是
由

解得



又直线的斜率为

于是
因此
由题意知,


又由点

故满足条件的直线


知识点
若不等式


正确答案
[﹣1,
解析
|2x﹣1|+|x+2|=
∴x=

∵不等式|2x﹣1|+|x+2|≥a2+
∴a2+

∴a2+

∴﹣1≤a≤
∴实数a的取值范围是[﹣1,
知识点
已知函数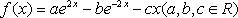
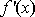
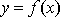
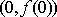
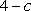
(1)确定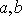
(2)若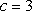
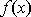
(3)若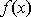

正确答案
(1)a=b=1
(2)f(x)在定义域R为均增函数
(3)c的取值范围为(4,+∞)
解析
(1)∵函数f(x)=ae2x﹣be﹣2x﹣cx(a,b,c∈R)
∴f′(x)=2ae2x+2be﹣2x﹣c,
由f′(x)为偶函数,
知f′(﹣x)=f′(x),
即2(a﹣b)(e2x+e﹣2x)=0,
即a=b,
又∵曲线y=f(x)在点(0,f(0))处的切线的斜率为4﹣c,
即f′(0)=2a+2b﹣c=4﹣c,
故a=b=1;
(2)当c=3时,f′(x)=2e2x+2e﹣2x﹣3≥2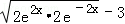
故f(x)在定义域R为均增函数;
(3)由(1)得f′(x)=2e2x+2e﹣2x﹣c,
而2e2x+2e﹣2x≥2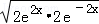
当c≤4时,f′(x)≥0恒成立,故f(x)无极值;
当c>4时,令t=e2x,方程2t+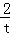
即f′(x)=0有两个根x1,x2,
当x∈(x1,x2)时,f′(x)<0,当x∈(﹣∞x1)∪(x2,+∞)时,f′(x)>0,
故当x=x1,或x=x2时,f(x)有极值,
综上,若f(x)有极值,c的取值范围为(4,+∞)。
知识点
已知函数f(x)是定义在R上的奇函数,当x≥0时,

正确答案
解析
当x≥0时,
f(x)=
由f(x)=x﹣3a2,x>2a2,得f(x)>﹣a2;
当a2<x<2a2时,f(x)=﹣a2;
由f(x)=﹣x,0≤x≤a2,得f(x)≥﹣a2。
∴当x>0时,
∵函数f(x)为奇函数,
∴当x<0时,
∵对∀x∈R,都有f(x﹣1)≤f(x),
∴2a2﹣(﹣4a2)≤1,解得:
故实数a的取值范围是
知识点
等差数列{an}的前n项和为Sn,已知a1=10,a2为整数,且Sn≤S4。
(1)求{an}的通项公式;
(2)设bn=
正确答案
见解析。
解析
(1)由a1=10,a2为整数,且Sn≤S4得
a4≥0,a5≤0,即10+3d≥0,10+4d≤0,解得﹣

∴d=﹣3,
∴{an}的通项公式为an=13﹣3n。
(2)∵bn==
∴Tn=b1+b2+…+bn=










知识点
某几何体的三视图如图所示,则该几何体的表面积为( )
正确答案
解析
由三视图知:几何体是直三棱柱消去一个同底的三棱锥,如图:
三棱柱的高为5,消去的三棱锥的高为3,
三棱锥与三棱柱的底面为直角边长分别为3和4的等腰直角三角形,
∵AB⊥平面BEFC,∴AB⊥BC,BC=5,FC=2,AD=BE=5,DF=5
∴几何体的表面积S=



故选:B。
知识点
若

正确答案
解析
由


知识点
扫码查看完整答案与解析