- 异面直线的判定
- 共23题
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
函数
正确答案
5
解析
略
知识点
在平面四边形ABCD中,AB=BD=CD=1,AB⊥BD,CD⊥BD,将△ABD沿BD折起,使得平面ABD⊥平面BCD,如图。
(1)求证:AB⊥CD;
(2)若M为AD中点,求直线AD与平面MBC所成角的正弦值。
正确答案
(1)证明:∵平面ABD⊥平面BCD,平面ABD∩平面BCD=BD,AB⊂平面ABD,AB⊥BD,
∴AB⊥平面BCD,又CD⊂平面BCD,∴AB⊥CD。
(2)建立如图所示的空间直角坐标系。
∵AB=BD=CD=1,AB⊥BD,CD⊥BD,
∴B(0,0,0),C(1,1,0),A(0,0,1),D(0,1,0),M
∴



设平面BCM的法向量

令y=﹣1,则x=1,z=1。
∴
设直线AD与平面MBC所成角为θ。
则sinθ=|cos



解析
空间角。
(1)利用面面垂直的性质定理即可得出;
(2)建立如图所示的空间直角坐标系,设直线AD与平面MBC所成角为θ,利用线面角的计算公式sinθ=|cos

知识点
若


正确答案
解析
设直线的倾斜角为

知识点
如图5,已知△ABC为直角三角形,∠ACB为直角.以AC为直径作半圆O,使半圆O所在平面⊥平面ABC,P为半圆周异于A,C的任意一点。
(1) 证明:AP⊥平面PBC
(2) 若PA=1,AC=BC=2,半圆O的弦PQ∥AC,求平面PAB与平面QCB所成锐二面角的余弦值。
正确答案
见解析。
解析

知识点
如图1,在Rt△ABC中,∠C=90°,BC=3,AC=6,D,E分别是AC,AB上的点,且DE∥BC,DE=2,将△ADE沿DE折起到△A1DE的位置,使A1C⊥CD,如图2.
(1)求证:A1C⊥平面BCDE;
(2)若M是A1D的中点,求CM与平面A1BE所成角的大小;
(3)线段BC上是否存在点P,使平面A1DP与平面A1BE垂直?说明理由
正确答案
见解析
解析




又

又


(2)如图建系



∴
设平面
则

∴
又∵
∴
∴
∴


(3)设线段



则
设平面

则
∴
假设平面

则



∵




知识点
如图,正方体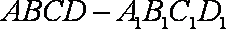
(1)求直线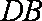
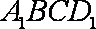
(2)求四棱锥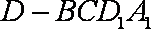
正确答案
(1)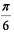
解析
解析:(1)以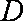
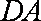
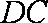
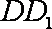
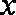
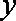
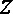
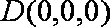
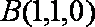
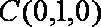
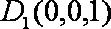
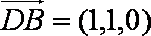
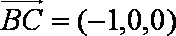

设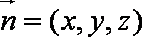
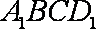
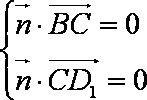
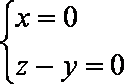
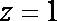
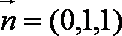
设直线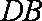
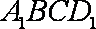
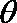
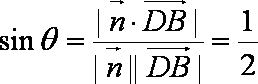
由于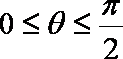
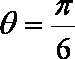
即直线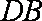
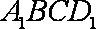
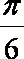
(2)由(1)得
所以点
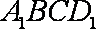
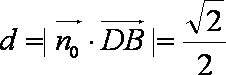
因为四边形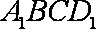
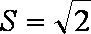
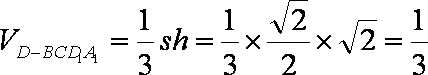
知识点
如右图,在△





正确答案
解析
略
知识点
一个几何体的三视图如图所示,该几何体的表面积是___________。
正确答案
解析
略
知识点
如图,在直三棱柱


(1)求四棱锥
(2)求异面直线AE与A1C所成的角。
正确答案
见解析
解析
(1)四棱锥


∴
(2)取B1C1的中点E1,连A1E1,E1C,
则AE∥A1E1,∴∠E1A1C是异面直线AE与A1C所成的角。…(8分)
由






所以异面直线AE与A1C所成的角为
知识点
扫码查看完整答案与解析