- 异面直线及其所成的角
- 共103题
如图,






(1)证明:
(2)如果


正确答案
见解析
解析
解析:(1)连






由







(2)取












由










注:用向量解相应给分。
知识点
已知三棱锥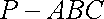
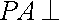
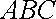
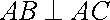
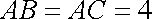
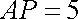
(1)求二面角
(2)把△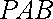

正确答案
见解析
解析
(1)解法一:设

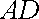


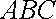




在等腰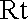
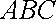
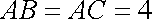
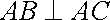
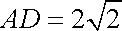
由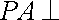
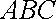

在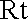
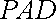
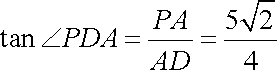
故二面角
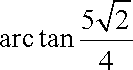
解法二:如图建立空间直角坐标系,可得各点的坐标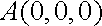
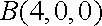
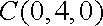
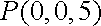
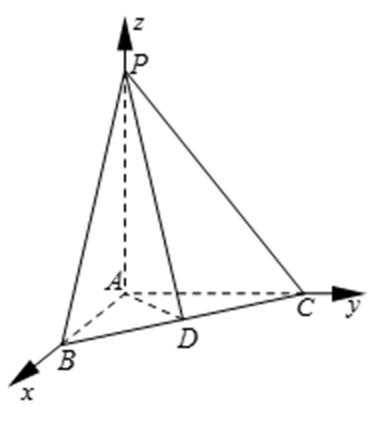
于是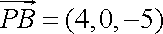
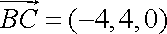
由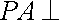
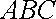
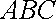
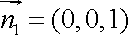
设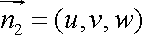

因为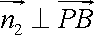
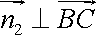
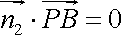
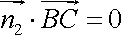
即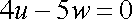
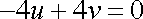
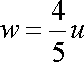

取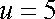
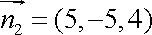
设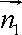
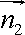
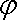
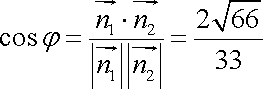
结合图可判别二面角
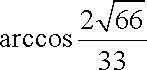
(2)由题设,所得几何体为圆锥,其底面半径为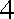

该圆锥的体积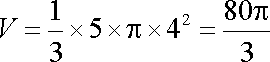
知识点
如图,在直三棱柱ABC-A1B1C1中,平面A1BC⊥侧面A1ABB1.
(1)求证:AB⊥BC;
(2)若直线AC与平面A1BC所成的角为θ,二面角B-A1C-A的大小为φ,当A1A=AC=2BC=2时,求sinθ·sinφ的值。
正确答案
见解析
解析
(1)如右图,作A在A1B上的射影D.
∵平面A1BC⊥侧面A1ABB1,且平面A1BC∩侧面A1ABB1=A1B,
∴AD⊥平面A1BC,又BC⊂平面A1BC, ∴AD⊥BC,
∵三棱柱ABC-A1B1C1是直三棱柱,∴AA1⊥底面ABC,∴AA1⊥BC.
又AA1∩AD=A,∴BC⊥侧面A1ABB1,AB
故AB⊥BC. ………6′
(2)〖法一〗联结CD,则由(1)知∠ACD是直线AC与平面A1BC所成的角,
取A1C的中点E,连AE,DE,∵A1A=AC,A1A⊥BC, ∴AE⊥A1C,
又AD⊥A1C,∴A1C⊥平面ADE,∴A1C⊥DE,
∴∠AED是二面角B-A1C-A的平面角。即∠ACD=θ,∠AED=φ,
∴

∵A1A=AC=2BC=2,∴
∴
〖法二〗由(1)知,以B为原点,建立如图所示的空间直角坐标,
则A(0,,0),C(1,0,0),A1 (0,,2),
∴

设平面A1BC的一个法向量为
平面AA1C的一个法向量为
则
取
由

∴

∴
知识点
如图,在四棱锥





(1)求证: AC⊥DE;
(2)已知二面角





正确答案
见解析
解析
解析: (1)证明:∵ 


∴
又∵
∴


∴ 
(2)分别以


由(1)知:平面


则根据

因为二面角A-PB-D的余弦值为


∴
设EC与平面PAB所成的角为



知识点
已知矩形







正确答案
解析
设圆柱下底面圆


由矩形



于是

又圆柱的体积

分别以直线

系

设异面直线





则
故异面直线


知识点
在三棱锥S—ABC中,底面是边长
底面ABC上的射影O恰是BC的中点,侧棱SA和底面成45°角。
(1)若D为侧棱SA上一点,当
(2) 求二面角S—AC—B的余弦值大小。
正确答案
见解析
解析
以O点为原点,OC为x轴,OA为y轴,OS为z轴建立空间直角坐标系,因为





所以O(0,0,0),C(

(1)设AD=a,则D(0,3-










解得a=2


所以
(2)因为


设平面ACS的法向量为n1=(x,y,z),
则
令z=1,则x=

而平面ABC的法向量为n2=(0,0,1),
所以cos<n1,n2>=
故所求二面角的余弦值的大小为
知识点
如图,五面体












(2)当


正确答案
见解析
解析
(1)当


证明:连结




∴



∵




(2)
建立空间直角坐标系




所以

设



令



所以


知识点
中国蓝球职业联赛(CBA)的总决赛采用七局四胜制,当两支实力水平相当的球队进入总决赛时,根据以往经验,第一场比赛中组织者可获票房收入

(1)组织者至少可以获得多少票房收入?
(2)决出胜负所需比赛场次的均值.
正确答案
见解析
解析
(1)设n为比赛的场数,
则



(2)(理)当







所以决出胜负的比赛场次的均值为6场. (12分)
知识点
如图所示,四面体ABCD中,AB⊥BD、AC⊥CD且AD =3。BD=CD=2。
(1)求证:AD⊥BC;
(2)求二面角B—AC—D的余弦值。
正确答案
见解析
解析
(1)证明:作AH⊥平面BCD于H,连接BH、CH、DH,
易知四边形BHCD是正方形,且AH=1,以D为原
点,以DB所在直线为x轴,DC所在直线为y轴,
以垂直于DB,
标系,如图所示,则B(2,0,0),C(0,2,0),
所以=



因此·=

(2)设平面ABC的法向量为n1=(x,y,z),则由n1⊥知:n1·=
同理由n1⊥知:n1·=
可取n1=
同理,可求得平面ACD的一个法向量为
∴cos〈n1,n2〉==
即二面角B—AC—D的余弦值为
知识点
在直三棱柱


(1)若异面直线


(2)设





正确答案
见解析
解析
解析:解法1:
(1)由三棱柱

如图1,因为




连接


在Rt△



又异面直线




于是
在Rt△



(2)设



由




而


故



在



在




在


令
因为


所以
故当


解法2:
建立如图2所示的空间直角坐标系
设







(1)因为异面直线



即


(2)由



设平面






于是
而
令
因为


所以
故当


知识点
扫码查看完整答案与解析