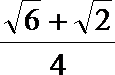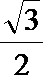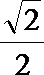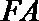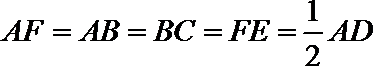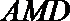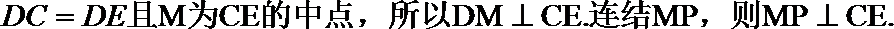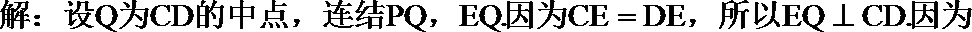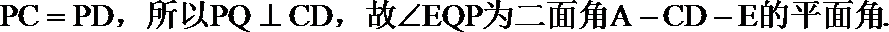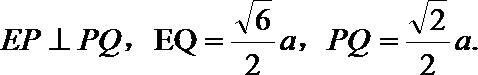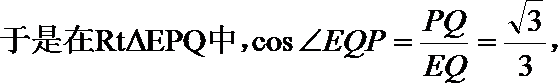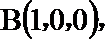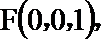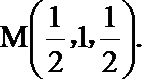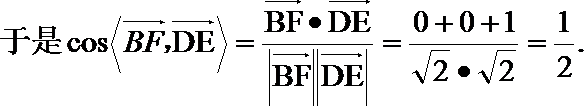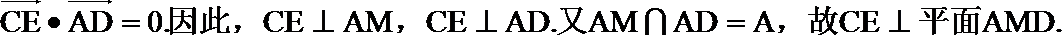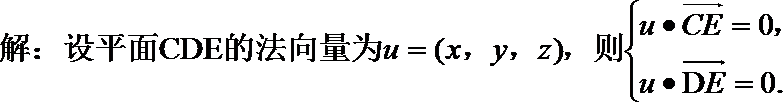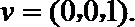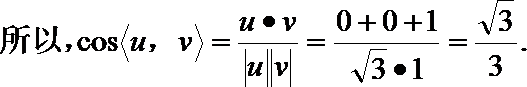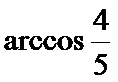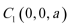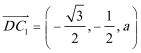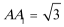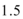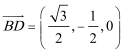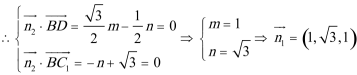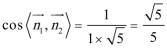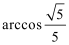- 异面直线及其所成的角
- 共103题
8．在正三棱锥
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
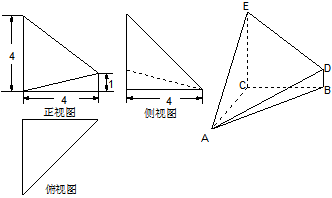
19．已知几何体A—BCED的三视图如图所示，其中俯视图和侧视图都是腰长为4的等腰直角三角形，正视图为直角梯形．
（1）求此几何体的体积V的大小;
（2）求异面直线DE与AB所成角的余弦值；
（3）试探究在DE上是否存在点Q，使得AQ
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
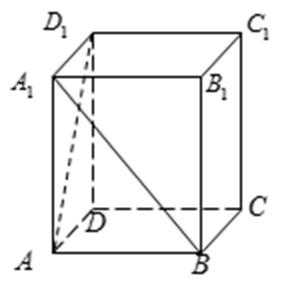
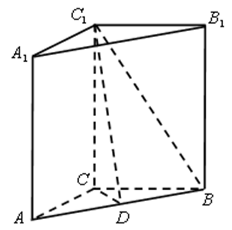
20．如图，在三棱柱
（1）求证：
（2）求棱
（3）在线段
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
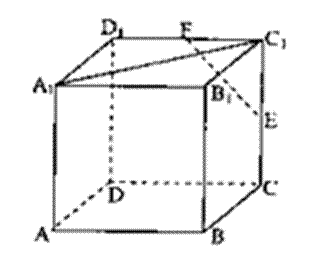
7．在正方体ABCD—A1B1C1D1中，E、F分别是棱CC1与D1C1的中点，则直线EF与A1C1所成角正弦值是（ ）
A1
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
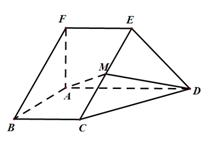
19.如图，在五面体
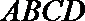
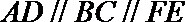
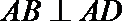
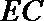
（I）求异面直线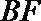
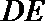
（II）证明平面
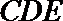
（III）求二面角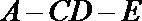
正确答案
方法一：
（Ⅰ）解：由题设知，BF//CE，所以∠CED（或其补角）为异面直线BF与DE所成的角。设P为AD的中点，连结EP，PC。因为FE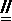
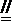
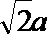
（II）证明：因为
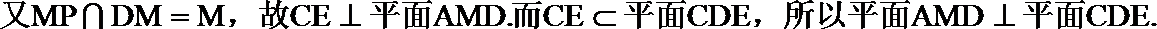
由（I）可得，
方法二：
如图所示，建立空间直角坐标系，
点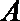
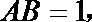
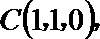
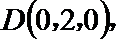
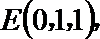
（I）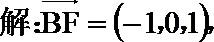
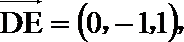
所以异面直线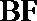
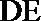
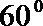
（II）证明：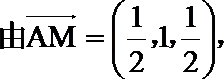
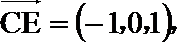
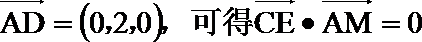
（III）
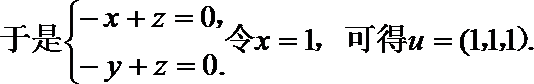
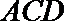
解析
解析已在路上飞奔，马上就到！
知识点
7．如图，正四棱柱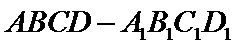
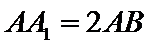
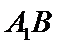
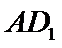
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
18．已知几何体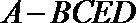
（Ⅰ）求此几何体的体积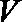
（Ⅱ）求异面直线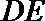
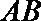
（Ⅲ）试探究在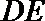
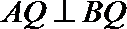
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
20．在直三棱柱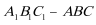
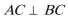
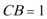
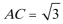
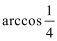
（1）求三棱柱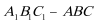
（2）求二面角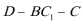
正确答案
（1）如图建立空间直角坐标系
设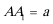
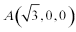
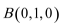
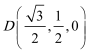
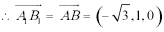
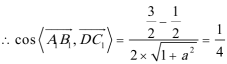
解得
可得：三棱柱
（2）显然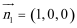
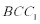
设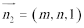
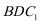
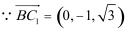
所以二面角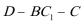
解析
解析已在路上飞奔，马上就到！
知识点
12．有六根细木棒，其中较长的两根分别为
A0
B
C0或
D以上皆不对
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
18．在斜三棱柱ABC—A1B1C1中，侧面A1ACC1⊥底面ABC，底面△ABC是边长为2的正三角形，A1A=A1C，A1A⊥A1C。
（1）求证：A1C1⊥B1C；
（2）求二面角B1—A1C—C1的大小。
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
扫码查看完整答案与解析