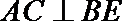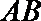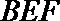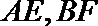- 异面直线及其所成的角
- 共103题
6.已知正四面体ABCD中,E是AB的中点,则异面直线CE与BD所成角的余弦值为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
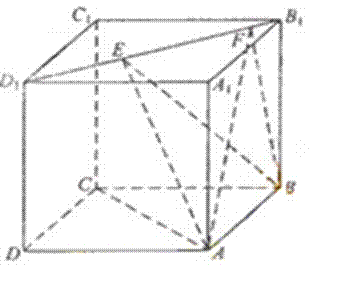
20.如图,在长方体



(1)求异面直线

(2)

正确答案
(1) 以




设





解二:三垂线定理;
解三:实在不会做就硬做
(2) 过











解二:或利用空间向量
解析
解析已在路上飞奔,马上就到!
知识点
18.过正方体





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.如图,在四棱锥ABCD-PGFE中,底面ABCD是直角梯形,侧棱垂直于底面,AB//DC,∠ABC=45o,DC=1,AB=2,PA=1.
(1)求PD与BC所成角的大小;
(2)求证:BC⊥平面PAC;
(3)求二面角A-PC-D的大小。
正确答案
(1)取的AB中点H,连接DH,易证BH//CD,且BD=CD
所以四边形BHDC为平行四边形,所以BC//DH
所以∠PDH为PD与BC所成角
因为四边形,ABCD为直角梯形,且∠ABC=45o, 所以⊥DA⊥AB
又因为AB=2DC=2,所以AD=1,
因为Rt△PAD、Rt△DAH、Rt△PAH都为等腰直角三角形,
所以PD=DH=PH=
(2)连接CH,则四边形ADCH为矩形,
∴AH=DC 又AB=2,∴BH=1
在Rt△BHC中,∠ABC=45o ,
∴CH=BH=1,CB=
∴AD=CH=1,AC=
∴AC2+BC2=AB2
∴BC⊥AC
又PA平面ABCD
∴PA⊥BC ……7分
∵PA∩AC=A
∴BC⊥平面PAC
(3)
如图,分别以AD、AB、AP为x轴,y轴,z轴建立空间直角坐标系,则由题设可知:
A(0,0,0),P(0,0,1),C(1,1,0),D(1,0,0),
∴

设m=(a,b,c)为平面PAC的一个法向量,即
设

同理设n=(x,y,z) 为平面PCD的一个法向量,求得n=(1,1,1)
∴
所以二面角A-PC-D为60o
解析
解析已在路上飞奔,马上就到!
知识点
20.已知,如图四棱锥













(1)求异面直线

(2)若



正确答案
解法一:(1)
由已知
∴PG=4
如图所示,以G点为原点建立空间直角坐标系o—xyz,则
B(2,0,0),C(0,2,0),P(0,0,4)
故E(1,1,0)
(2)设F(0,y , z)
在平面PGC内过F点作FM⊥GC,M为垂足,则
解法二:
(1)由已知
∴PG=4
在平面ABCD内,过C点作CH//EG交AD于H,连结PH,则∠PCH(或其补角)就是异面直线GE与PC所成的角.
在△PCH中,
由余弦定理得,cos∠PCH=
(2)在平面ABCD内,过D作DM⊥GC,M为垂足,连结MF,又因为DF⊥GC
∴GC⊥平面MFD, ∴GC⊥FM
由平面PGC⊥平面ABCD,∴FM⊥平面ABCD ∴FM//PG
由GM⊥MD得:GM=GD·cos45°=
解析
解析已在路上飞奔,马上就到!
知识点
8.如图,正方体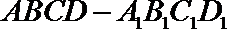
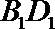
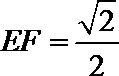
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3. 如图,E、F分别是三棱锥P-ABC的棱AP、BC的中点,PC=10,AB=6,EF=7,则异面直线AB与PC所成的角为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.如图,在△ABC和△AEF中,B是EF的中点,AB=EF=1,



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20. 如图,沿河边AB建一水站P供甲、乙两个学校共同使用,已知学校甲离河边1千米,学校乙离河边2千米,而甲、乙两校相距
(1)设


(2)问水站P建在什么位置,购买水管的费用最低?
正确答案
(1)由题意:AB=3,CP=
故:
(2)
即:
化简:
答:
解析
解析已在路上飞奔,马上就到!
知识点
4. 设集合


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析