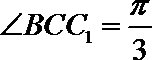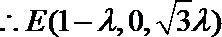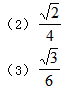- 异面直线及其所成的角
- 共103题
19.如图,




(Ⅰ)当平面


(Ⅱ)当

正确答案
(Ⅰ)取


因为

当平面

因为平面

所以

由已知可得
在

(Ⅱ)当


证明如下:
①当


所以


②当


又因

又


由


综上所述,总有
解析
解析已在路上飞奔,马上就到!
知识点
22.已知椭圆C过点









(1)求椭圆C的方程; 
(2)求直线

(3)求
正确答案
(1)由题意得
则
所以椭圆

(2)

则
故
因为直线
所以
由于
(3)因为直线



设


则
所以

解析
解析已在路上飞奔,马上就到!
知识点
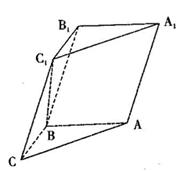
19. 如图,在三棱柱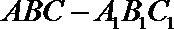
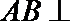
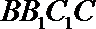
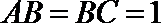
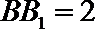
(1)求证: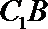
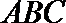
(2)设λ=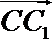
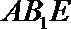
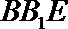
正确答案
(1)因为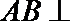
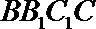
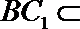
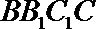
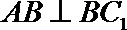
在
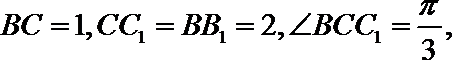
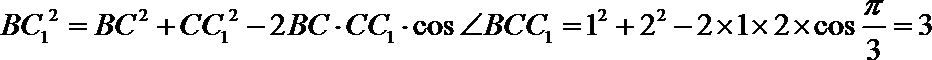
所以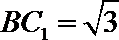
故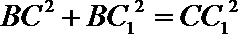
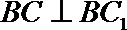
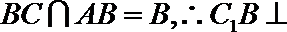
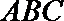
(2)由(1)可知,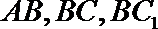
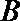
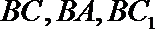
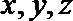
则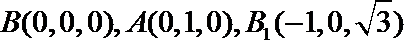
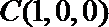
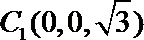
所以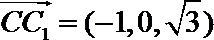
所以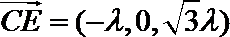
则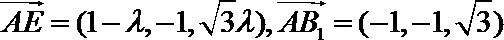
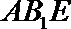
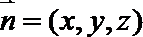
则由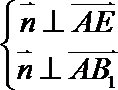
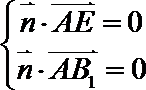
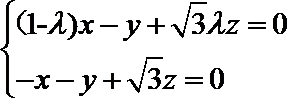
令
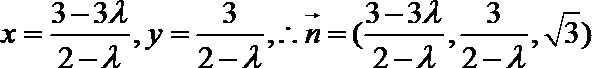
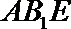
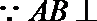
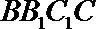
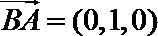

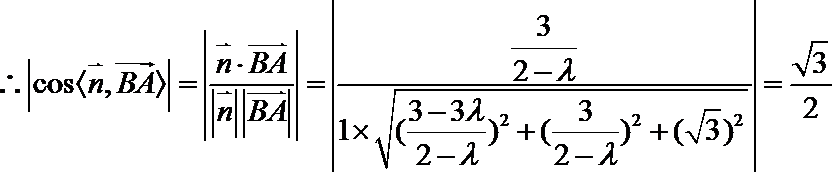
两边平方并化简得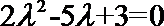
所以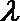
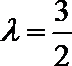
解析
解析已在路上飞奔,马上就到!
知识点
16. 过一定点的互相垂直的两条直线




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
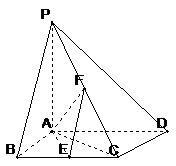
19.如图,已知四棱锥P—ABCD,底面ABCD为菱形,PA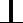
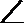
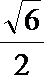
(1) 证明:AE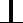
(2) 求异面直线PB与AC所成的角的余弦值;
(3) 若AB=2,求三棱锥P—AEF的体积。
正确答案
(1)略
解析
解析已在路上飞奔,马上就到!
知识点
20.如图,在四棱锥







( 1)求证:平面

(2)设




正确答案
(1)










(2) 

又


建系







平面




解析
解析已在路上飞奔,马上就到!
知识点
18.如图,直三棱柱




(Ⅰ)证明:
(Ⅱ)求二面角
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.在一个给定的正(2n+1)边形的顶点中随机地选取三个不同的顶点,任何一种选法的可能性是相等的,则正多边形的中心位于所选三个点构成的三角形内部的概率为_______.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
23. 已知四棱锥







(1)求异面直线

(2)若

(3)是否存在


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.已知直三棱柱ABC-A1B1Cl中,
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析