- 异面直线及其所成的角
- 共103题
12.正四棱柱ABCD-A1B1C1D1中,底面边长为1,侧棱长为2,则异面直线AC1与B1C所成角的余弦值是 .
正确答案
解析
本题属于空间角的计算问题,题目的难度较小。注意利用向量法比推理法简单。
考查方向
本题主要考查了立体几何的空间角的问题。
易错点
本题必须注意正四棱柱的性质,忽视则会出现错误。
知识点
16.一个几何体由八个面围成,每个面都是正三角形,有四个顶点在同一平面内且为正方形,从该几何体的12条棱所在直线中任取2条,所成角为60°的直线共有 对.
正确答案
48
解析
该几何体是两个全等的正四棱锥底面重合,对接成的组合体,其中侧面均为正三角形。先从相交直线入手,成60°的直线有24对,在考虑异面直线,成60°的直线有24对也有24对,所以共计48对
考查方向
解题思路
分两种类,一类是求所成角为60°的相交直线的对数,另一类是求所成角为60°的异面直线的对数。
易错点
一是几何体的结构想象不出来,还有就是所成角为60°的直线有相交直线,也有异面直线,异面直线可能会出现重复或遗漏。
知识点
16.在下列命题中:
①存在一个平面与正方体的12条棱所成的角都相等;
②存在一个平面与正方体的6个面所成较小的二面角都相等;
③存在一条直线与正方体的12条棱所成的角都相等;
④存在一条直线与正方体的6个面所成的角都相等.
其中真命题为____________
正确答案
①②③④.
解析
命题①, 我们取过D点的三条棱为例,很显然存在一个过D点的面与这三条棱所成的角的相等的。
命题②,同样我们取以D点为顶点的三个面,也同样存在一个面与这三个面的角都是相等的;
命题③,正方体的任何一条体对角线都满足与各棱所成的角都相等;
命题④,以D点为顶点,在对角面

考查方向
解题思路
根据空间图形分析,注意正方体中的6个面实际上是3组两两平行的面,12条棱也是3组互相平行的线
易错点
只考虑到了正方体的体对角线和某些特殊的现或面,如果它们不满足题目要求就认为没有这样的线或面
知识点
18.如图,在四棱锥





(1)求证:平面
(2)若二面角



正确答案
见解析
解析
(1)由



于是
又





(2)以
则
设

即


依题意有
于是
设直线


则直线


考查方向
解题思路
利用面面垂直证明线面垂直,利用余弦定理表示出平面角的值
易错点
找不到二面角,辅助线作不出来
知识点
7.三棱柱ABC-A1B1C1中,底面是边长为
正确答案
解析
以A为坐标原点,AC的垂线为X轴,AC为Y轴,AA1为Z轴建立空间直角坐标第,进而点B坐标为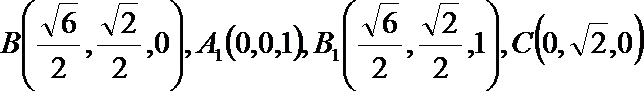
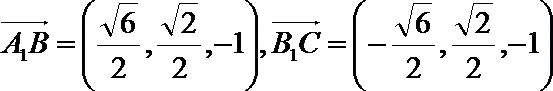
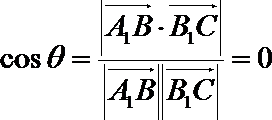
考查方向
本题主要考查了立体几何异面直线所成角问题,在近几年的各省高考题出现的频率较高。
易错点
1、本题如用传统方法易卡在作异面直线所成角。
2、用向量法易在一些点的坐标计算上难住。
3、异面直线所成角的范围。
知识点
扫码查看完整答案与解析
















