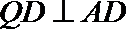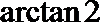- 异面直线及其所成的角
- 共103题
11.平面a过正方体ABCD-A1B1C1D1的顶点A,a//平面CB1D1,

正确答案
知识点
18.如图,在已A,B,C,D,E,F为顶点的五面体中,面ABEF为正方形,AF=2FD,

(I)证明:平面ABEF
(II)求二面角E-BC-A的余弦值.
正确答案
(1) 证明
∵ 平面ABEF为正方形
∴ AF⊥PE
又∵ ∠AFD=90°即AF⊥FD
而FE,FD 
∴ AF⊥平面EFDC
又AF
∴平面ABEF ⊥平面EFDC
(II) ∵ 二面角D-AF-E的平面角为60°
∴ ∠DFE=60°
在平在面EFDC内作DO⊥EF 于点O, 则DO⊥平面ABEF.
令AF=4,则DF=2.在△ADF 中, OF=1,OD=
在平面ABEF 内作OA//AF 交AB 于M , 则OM ⊥EF
以O为原点,OM,OE,OD 分别为x,y,z轴建立如图所示空间直角坐标系,
则E(0,3,0),B(4,3,0),C(0,4, 
直角坐标系,则E(0,3,0),B(4,3,0),C(0,4, 
设平面EBC法向量为

∴
(II)
设平面BCA法向量为
则
∴
∴
∴ 二面角E-BC-A的余弦值为
知识点
若
正确答案
解析
能存在平面

因为平面

则直线

考查方向
本题主要考查异面直线的概念以及空间想象力,是常考题型
易错点
对空间想象力要求较高,需要一定的基础
知识点
12.正四棱柱ABCD-A1B1C1D1中,底面边长为1,侧棱长为2,则异面直线AC1与B1C所成角的余弦值是 .
正确答案
解析
试题分析:本题属于空间角的计算问题,题目的难度较小。注意利用向量法比推理法简单。
考查方向
本题主要考查了立体几何的空间角的问题。
解题思路
本题考查异面直线所成的角,解题步骤如下:
利用向量法,建立空间直角坐标系,写出向量AC1和B1C的坐标,再用夹角的余弦公式求解。
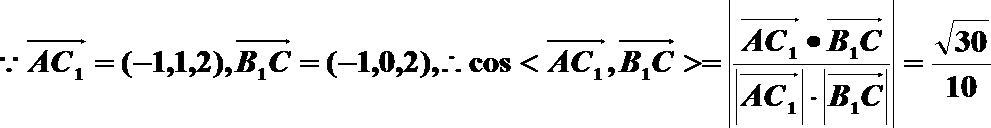
易错点
本题必须注意正四棱柱的性质,忽视则会出现错误。
知识点
在三棱锥
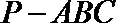
正确答案
解: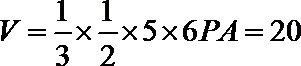
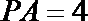
取PC的中点为D,连结AD,DQ,
则
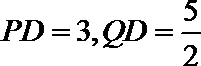
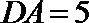
因为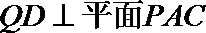
所以
所以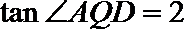
直线PB,AQ所成的角为
解析
本题属于空间几何体的基本问题,题目的难度是简单,本题的关键是通过添加辅助线找出异面直线PB,AQ所成的角,
考查方向
本题考查了空间几何体的体积与异面直线的综合应用
易错点
1、找异面直线PB,AQ所成的角容易出错
知识点
扫码查看完整答案与解析