• 职业资格类
  • 建筑类
  • 学历类
  • 财会类
  • 医药类
  • 全部考试
职业资格类
建筑类
学历类
财会类
计算机类
公务员
医药类
  • 圆与圆的位置关系及其判定
  • 共52题
  • 圆与圆的位置关系及其判定
  • 共52题

热门试卷

X 查看更多试卷
1
题型： 单选题
|
单选题 · 5 分

等差数列中，公差，且成等比数列，则          （   ）

A

B

C

D

正确答案

B

解析

略

知识点

圆与圆的位置关系及其判定
1
题型：填空题
|
填空题 · 5 分

如图3，AB是⊙O的直径，BC是⊙O的切线，AC与⊙O

交于点D，若BC=3，，则AB的长为______.

正确答案

4

解析

略

知识点

圆与圆的位置关系及其判定
1
题型：简答题
|
简答题 · 14 分

已知函数，函数的导函数，且，其中为自然对数的底数。

（1）求的极值；

（2）若，使得不等式成立，试求实数的取值范围；

（3） 当时，对于，求证：，

正确答案

见解析

解析

(1) 函数的定义域为，。

当时，，在上为增函数，没有极值；……………1分

当时，，

若时，；若时，

存在极大值，且当时，

综上可知：当时，没有极值；当时，存在极大值，且当时，  …………………………………………………………4分

(2) 函数的导函数，

，，……………………………………5分

，使得不等式成立，

，使得成立，

令，则问题可转化为：

对于，，由于，

当时，，，，

，从而在上为减函数，

………………………………………………………………………………………9分

(3)当时，，令，则，

，且在上为增函数

设的根为，则，即

当时，，在上为减函数；当时，，在上为增函数，

，，

由于在上为增函数，

 …………………………………………………………………………14分

知识点

圆与圆的位置关系及其判定
1
题型：填空题
|
填空题 · 4 分

在中, 角所对的边长,的面积为,外接圆半径，则的周长为_______

正确答案

解析

略

知识点

圆与圆的位置关系及其判定
1
题型： 单选题
|
单选题 · 5 分

如图，双曲线的中心在坐标原点，

分别是双曲线虚轴的上、下顶点，是双曲线的左顶点，为双曲线的左焦点，直线与相交于点.若双曲线的离心率为2，则的余弦值是(   )

A

B

C

D

正确答案

C

解析

略

知识点

圆与圆的位置关系及其判定
1
题型：填空题
|
填空题 · 5 分

给出以下四个命题：

①已知命题；命题.则命题是真命题；

②圆恰有2条公切线；

③在某项测量中，测量结果服从正态分布.若内取值的概率为0.4，则在内取值的概率为0.8；

④某企业有职工150人，其中高级职称15人，中级职称45人，一般职员90人，若用分层抽样的方法抽出一个容量为30的样本，则一般职员抽出20人.

其中正确命题的序号为_________（把你认为正确的命题序号都填上）

正确答案

解析

略

知识点

命题的真假判断与应用圆与圆的位置关系及其判定正态分布曲线的特点及曲线所表示的意义分层抽样方法
1
题型：填空题
|
填空题 · 5 分

如图，是⊙的直径，直线切⊙于点，且与延长线交于点，若，，则=   。

正确答案

解析

略

知识点

圆与圆的位置关系及其判定
1
题型： 单选题
|
单选题 · 13 分

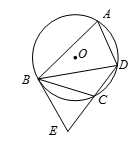
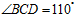
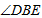
如图，A,B,C,D是⊙O上的四个点，过点B的切线与DC的延长线交于点E.若，则=

A

B

C

D

正确答案

B

解析

略

知识点

圆与圆的位置关系及其判定
1
题型：简答题
|
简答题 · 12 分

已知函数。

（1）讨论函数在定义域内的极值点的个数；

（2）若函数在处取得极值，对,恒成立，求实数的取值范围；

（3）当，证明：

（4）当且时，试比较的大小，

正确答案

见解析。

解析

（1），当时，在上恒成立，函数 在单调递减，∴在上没有极值点；

当时，得，得，

∴在上递减，在上递增，即在处有极小值。

∴当时在上没有极值点，

当时，在上有一个极值点。

（2）∵函数在处取得极值，∴，

∴，

令，可得在上递减，在上递增，

∴，即。

（3）证明：，

令，则只要证明在上单调递增，

又∵，

显然函数在上单调递增。 

∴，即，

∴在上单调递增，即，

∴当时，有。

知识点

圆与圆的位置关系及其判定
1
题型：简答题
|
简答题 · 12 分

已知

（1）求函数的单调增区间

（2）在中，分别是角的对边，且 ，求的面积。

正确答案

（1）

（2）

解析

（1）因为==

==                       …………（3分）

所以函数的单调递增区间是[]（）……………（5分）

（2）因为=，所以,又，所以，从而

在中，∵   ∴1=b2+c2-2bccosA,即1=4-3bc.故bc=1………（10分）

从而S△ABC=…………（12分）

知识点

圆与圆的位置关系及其判定
继续学习 学习下一知识点
下一知识点 : 两圆的公切线条数及方程的确定
百度题库 > 高考 > 理科数学 > 圆与圆的位置关系及其判定

扫码查看完整答案与解析

  • 上一题
  • 1/10
  • 下一题