- 圆与圆的位置关系及其判定
- 共52题
在直角坐标系










(1)求

(2)在以


正确答案
见解析。
解析
(1)曲线

曲线

两圆的公共弦所在直线为



(2)曲线

曲线

设






所以
知识点
已知数列

(1)求数列
(2)数列满足

正确答案
见解析。
解析
(1)
当
两式相减得:
所以数列

(2)
=
知识点
不等式



(1)求函数
(2) 求实数的取值范围。
正确答案
见解析
解析
(1)对于上面的不等式小川同学设



原不等式化为:

即
整理得
因为 


令
则函数

所以


即知

知识点
已知圆





(1)将圆

(2)圆

正确答案
见解析
解析
解析:(1)由
又∵ρ=2cos(θ+)=cosθ-sinθ,
∴ρ2=ρcosθ-ρsinθ.
∴x2+y2-x+y=0,即
(2)圆心距
由得,A(1,0),B
∴ 
知识点
已知数列{an} (n=1,2,3,…2012),圆C1:x2+y2-4x-4y=0 ,圆C2:x2+y2-2anx-2a2013-ny=0 ,若圆C2平分圆C1的周长,则{an}的所有项的和为 。
正确答案
解析
设球半径












知识点
选做题(14、15题,只能从中选做一题,两题都选只计算14题得分)
14.(几何证明选讲选做题)
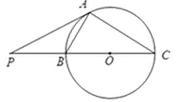
如图,PA是圆O的切线,切点为A,PO交圆O于B,C两点,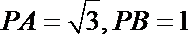
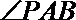
15.(坐标系与参数方程选做题)
在直角坐标平面内,以坐标原点O为极点、x轴的非负半轴为极轴建立极坐标系,已知点M的极坐标为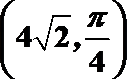
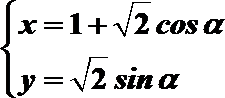
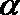
正确答案
14.
15.
解析
解析已在路上飞奔,马上就到!
知识点
9.如图为一个几何体的三视图,主视图和左视图均为矩形,俯视图中曲线部分为半圆,尺寸如图,则该几何体的表面积为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.已知函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.对于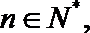
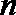
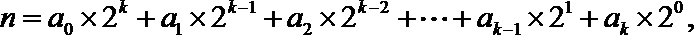
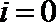
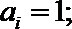
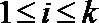
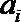
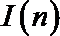
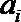
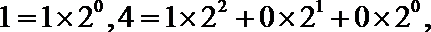
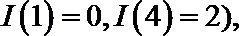
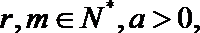
(1)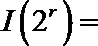
(2)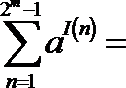
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4. 已知向量



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析