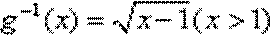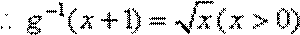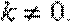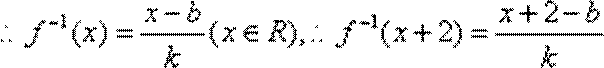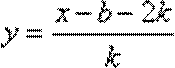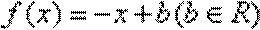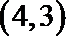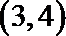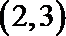- 对数与对数函数
- 共360题
10.设函数







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.函数




正确答案
(1,3)
解析
解析已在路上飞奔,马上就到!
知识点
22.已知函数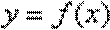


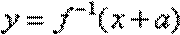
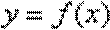
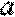
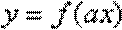


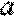
(1)判断函数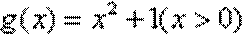
(2)求所有满足“2和性质”的一次函数;
(3)设函数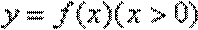
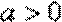
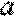

正确答案
(1)函数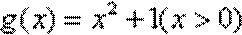
而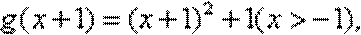
故函数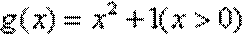
(2)设函数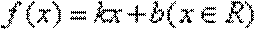
而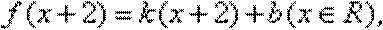
由“2和性质”定义可知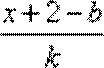

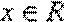
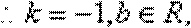
(3)设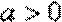

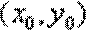
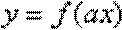
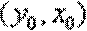

故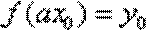
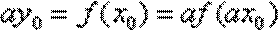
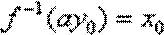
令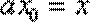

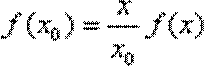
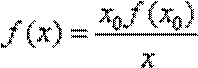
综上所述,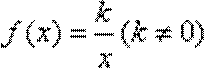
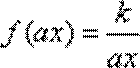
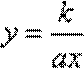
而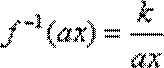


解析
解析已在路上飞奔,马上就到!
知识点
14.设a > 1,函数
(1)求

(2) 若
(3)若
正确答案
解:
(1) 由
∴
∴
(2) ∵ a > 1 ∴ 
∴ 
∴ 
∴
(3)
要使
只需
∴
∴
因此,a的取值范围为
解析
解析已在路上飞奔,马上就到!
知识点
10.已知函数




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.已知向量

(1)求出

(2)

(3)设



正确答案
(1)
其振幅为

(2)可由



(3)由
∵ 


∴
解析
解析已在路上飞奔,马上就到!
知识点
15. 有四个命题:
①函数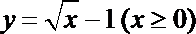
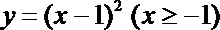
②函数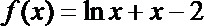
③函数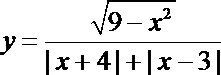
④若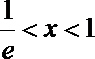
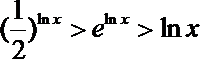
其中真命题的序号是________.
正确答案
③④
解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数
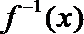
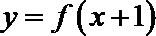
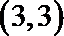
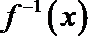
正确答案
解析
由f(x)恒过(4,3)得函数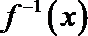
考查方向
本题主要考查反函数及图像平移
解题思路
1、求出f(x)所过定点;
2、利用对称性求解,即可得到结果。
A选项不正确,C选项不正确,D选项不正确,所以选B选项。
易错点
本题易在代点时发生错误。
知识点
5.若函数




正确答案
解析
∵函数


∴以




∴所求解析式为
考查方向
本题考查函数的图像变换,是容易题.
解题思路
函数









易错点
混淆各种函数图像变换.
知识点
16.设函数




正确答案
2
解析
设








考查方向
解题思路
本题考查函数图象的对称性,解题步骤如下:
法—:
1、由点


2、所以设



法二:
由点





易错点
1、本题易在解题思路上受阻。
2、点关于线对称的计算上和指数运算上。
知识点
扫码查看完整答案与解析