对数与对数函数
共360题

对数与对数函数
共360题

热门试卷

X 查看更多试卷

题型：单选题

单选题 · 4 分

16．已知函数．若，且，则的取值范围是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

换底公式的应用对数函数的图像与性质

题型：填空题

填空题 · 4 分

3．若，则的取值范围是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

换底公式的应用

题型：单选题

单选题 · 5 分

18．a＞0，a≠1，函数f（x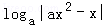）=在[3，4]上是增函数，则a的取值范围是（　　）

A或a＞1

Ba＞1

D或a＞1

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

换底公式的应用

题型：简答题

简答题 · 12 分

17.在中，，，分别是三内角A，B，C所对的三边，已知．

（1）求角A的大小；

（2）若，试判断的形状．

正确答案

（1），所以，得到

（2）∵ ∵

∴，

即，得到，

为等边三角形

解析

解析已在路上飞奔，马上就到！

知识点

换底公式的应用

题型：简答题

简答题 · 15 分

22．对任意,给定区间,设函数表示实数与的给定区间内整数之差的绝对值．

（1）当的解析式；当Z）时，写出用绝对值符号表示的的解析式；

（2）求的值，判断函数R）的奇偶性,并证明你的结论；

（3）当时，求方程的实根．（要求说明理由,）

正确答案

（1）当时，由定义知：与0距离最近，，

当时，由定义知：最近的一个整数，故

。

（2）

对任何R，函数都存在，且存在Z，满足Z）

即Z）．

由（Ⅰ）的结论，即是偶函数．

（3）解：

①当没有大于1的实根；

②容易验证为方程的实根；

③当

设

则

所以当为减函数，所以方程没有的实根；

④当

设为减函数，，

所以方程没有的实根．

综上可知，若有且仅有一个实根，实根为1．

解析

解析已在路上飞奔，马上就到！

知识点

换底公式的应用

题型：填空题

填空题 · 4 分

12．已知函数的图像如图所示，则（）．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

换底公式的应用

题型：填空题

填空题 · 5 分

11．设复数，其中，则______．

正确答案

-2/5

解析

解析已在路上飞奔，马上就到！

知识点

换底公式的应用

题型：填空题

填空题 · 4 分

11．．

正确答案

-1

解析

解析已在路上飞奔，马上就到！

知识点

换底公式的应用

题型：单选题

单选题 · 5 分

7．一个社会调查机构就某地居民的月收入调查20000人，并根据所得数据画出了样本频率分布直方图，为了分析居民的收入与年龄、学历、职业等方面的关系，按月收入用分层抽样方法抽样，若从月收入（元）段中抽取了30人，则在这20000人中共抽取的人数为（）

A200

B20000.

C100

D40

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

换底公式的应用

题型：单选题

单选题 · 3 分

（2012•六盘水）下列图形中既是中心对称图形，又是轴对称图形的是（　　）

A正三角形 B．平行四边形 C．等腰梯形 D．正方形

正确答案

解析

根据轴对称图形与中心对称图形的概念对各选项图形分析判断即可解答．

A、正三角形不是中心对称图形，是轴对称图形，故本选项错误；

B、平行四边形是中心对称图形，不是轴对称图形，故本选项错误；

C、等腰梯形不是中心对称图形，是轴对称图形，故本选项错误；

D、正方形是中心对称图形，也是轴对称图形，故本选项正确．

故选D．

本题考查了中心对称图形与轴对称图形，掌握中心对称图形与轴对称图形的概念：

轴对称图形的关键是寻找对称轴，图形两部分沿对称轴折叠后可重合；

中心对称图形是要寻找对称中心，旋转180度后与原图重合是解题的关键．

知识点

换底公式的应用

继续学习学习下一知识点

下一知识点 : 函数的图象

百度题库 > 高考 > 理科数学 > 对数与对数函数

扫码查看完整答案与解析