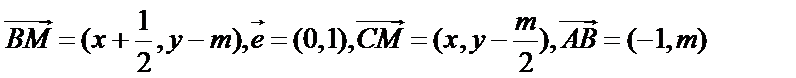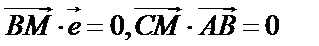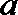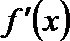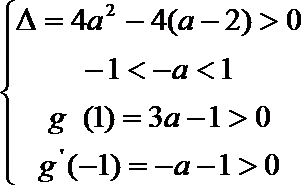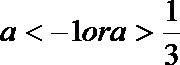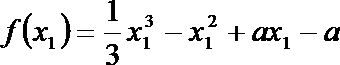- 对数与对数函数
- 共360题
设函数f(x)=(x-1)3-ax-b,x∈R,其中a,b∈R。
(I)求f(x)的单调区间;
(II)若f(x)存在极点x0,且f(x1)=f(x0),其中x1≠x0,求证:x1+2x0=3;
(III)设a>0,函数g(x)=∣f(x)∣,求证:g(x)在区间[0,2]上的最大值不小于
正确答案
(Ⅰ)解:由

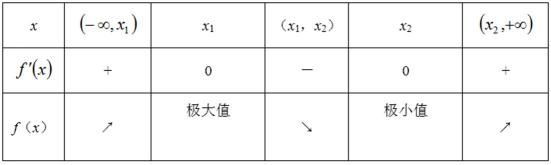
下面分两种情况讨论:
(1)当



(2)当



当


所以



(Ⅱ)证明:因为




进而
又






(Ⅲ)证明:设




(1)当








(2)当



所以



(3)当



所以



综上所述,当



知识点
16.已知


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.已知向量

(1)求函数
(2)当


正确答案
(1)

由

(2)

所以
解析
解析已在路上飞奔,马上就到!
知识点
20.在平面直角坐标系中,已知点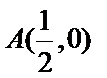
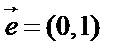
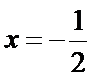

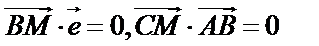
(1)试求动点M的轨迹E的方程;
(2)设点P是轨迹E上的动点,点R、N在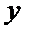
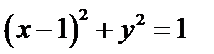
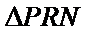
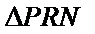
正确答案
(1)设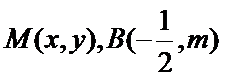
则
由
得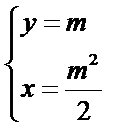
所以动点M的轨迹E的方程为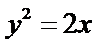
(2)设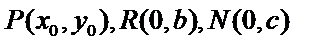
且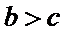
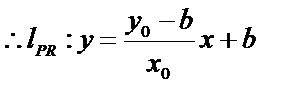
即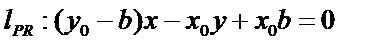
由相切得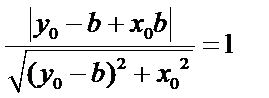
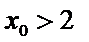
化简得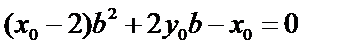
同理得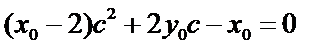
所以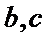
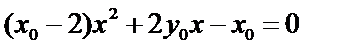
所以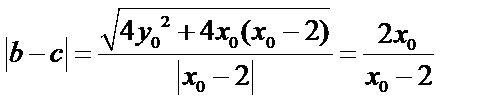
有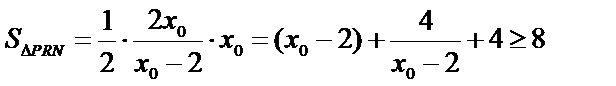
当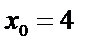
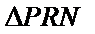
解析
解析已在路上飞奔,马上就到!
知识点
14.若


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
22. 已知函数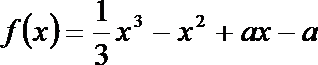
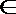
(1)当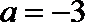
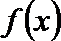
(2)设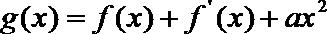
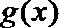
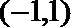
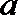
(3)若函数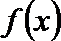
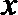
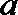
正确答案
解:(1)当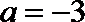
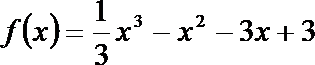
∴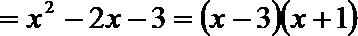
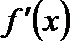
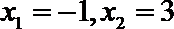
当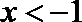
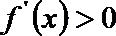
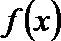
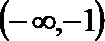
当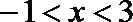
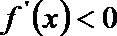
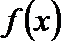
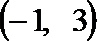
当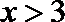
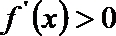
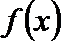
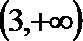
问题转化为方程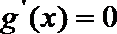
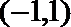
∴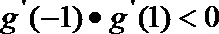
解得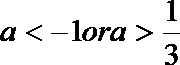
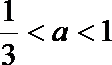
(3) ∵ 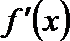
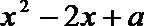
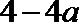
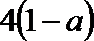
① 若a≥1,则△≤0, ∴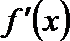
∴ f(x)在R上单调递增 .
∵f(0)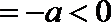
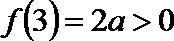
∴当a≥1时,函数f(x)的图象与x轴有且只有一个交点.
当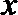
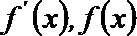
∵
∴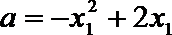
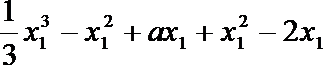
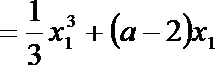
解析
解析已在路上飞奔,马上就到!
知识点
16.函数




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.如果函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
已知



正确答案
解析
略。
知识点
设
正确答案
解析
略
知识点
扫码查看完整答案与解析