- 立体几何与空间向量
- 共3353题
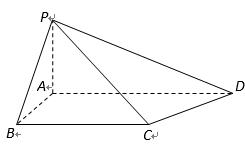
如图,在四棱锥









(1)求证:

(2)若点




正确答案
见解析
解析
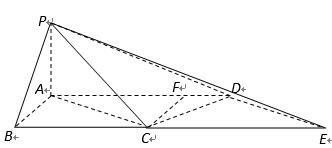
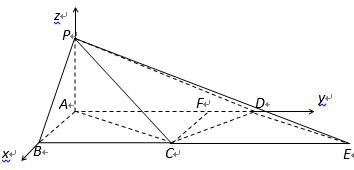
解法一:取




则









(2)设

设平面
令

设两个法向量的夹角为




解法二:(1)因为底面


又







(2)因为点


所以

过



因为



因为
在


知识点
某几何体的三视图如右图所示,其中正视图是腰长为2的等腰三角形,侧视图是半径为1的半圆,该几何体的体积为
正确答案
解析
由三视图可知该几何体是圆锥沿轴截面截成两部分,然后把截面放在平面上,底面相对接的图形(如图),圆锥的底面半径为1,母线长为2,故圆锥的高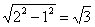
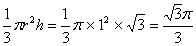
知识点
若非零向量




正确答案
解析
由题意得



知识点
如图甲,△ABC是边长为6的等边三角形,E,D分别为AB,AC靠近B,C的三等分点,点G为BC边的中点,线段AG交线段ED于点F,将△AED沿ED翻折,使平面AED⊥平面BCDE,连接AB,AC,AG,形成如图乙所示的几何体,

(1)求证:BC⊥平面AFG;
(2)求二面角
正确答案
见解析。
解析
(1)在图甲中,由△ABC是等边三角形,E,D分别为AB,AC的三等分点,点G为BC边的中点,
易知DE⊥AF,DE⊥GF,DE//BC,(2分)
在图乙中,因为DE⊥AF,DE⊥GF,AF
又DE//BC,所以BC⊥平面AFG,(4分)
(2)因为平面AED⊥平面BCDE,平面AED
所以FA,FD,FG两两垂直。
以点F为坐标原点,分别以FG,FD,FA所在的直线为




所以

设平面ABE的一个法向量为
则

取



显然
所以
又由图知二面角


知识点
已知向量


(1)求函数
(2)记△





正确答案
见解析
解析
(1)

所以
递减区间是
(2)由


当




当




知识点
在四边形




(1)求
(2)求四边形
正确答案
见解析。
解析
(1)
如图,连结

在
在
由
从而
(2)由(1)可知
所以
知识点
如图,在四棱锥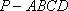
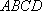
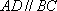
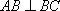
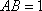
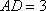
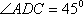
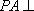
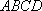
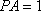
(1)异面直线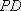
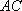
(2)四棱锥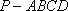
正确答案
见解析
解析
(1)连接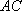
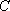
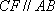
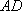
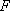
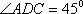
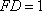
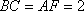
解法1:延长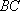
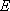
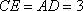
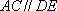
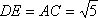
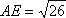
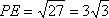
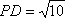
在△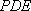
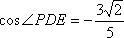
所以,异面直线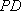
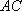
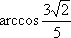
解法2:建立如图所示的空间直角坐标系.
则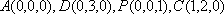
所以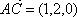
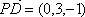
设异面直线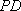
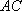
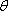
则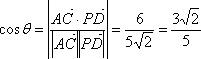
所以异面直线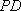
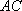
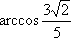
(2)底面梯形面积为

所以,四棱锥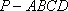
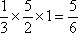
知识点
正三棱柱



(1)求侧棱
(2)求二面角
正确答案
见解析。
解析
(1)取





(2)过





连接

余弦值为
知识点
如图6,已知动圆







(1)求曲线
(2)设





① 证明:直线
② 记曲线








正确答案
见解析。
解析
(1)(法1)设


且点


所以
且圆

由题意,动圆

所以

所以曲线

(法2)因为动圆




连结





过点





在直角梯形

即动点


又动点


所以动点


故动点


所以曲线

(2)①(法1)由题意,直线
设直线




因为


所以


由
解之得

所以点

以



所以直线

(法2)因为




又点





而直线

所以它们的斜率互为相反数,即

所以直线

②(法1)由①可知,




整理得
设点





所以




所以

点


当

注意到


所以,点

(法2)由①可知,
若点



则曲线


设


消去

令△

代入方程组,解得

所以,点

(法3)因为抛物线


由图6-4可知,当直线







从而




由抛物线

得

所以抛物线


所以曲线段


即点

所以,点

知识点
已知三棱锥的俯视图与侧视图如图所示,俯视图是边长为2的正三角形,侧视图是有一直角边为2的直角三角形,则该三棱锥的正视图可能为
正确答案
解析
由于空间几何体的正视图和侧视图“高平齐”,故正视图的高一定是2,由于正视图和俯视图“长对正”,故正视图的底面边长为2,又根据侧视图可知这个空间几何体最前面的面垂直于底面,这个面遮住了后面的一个侧棱,综上可知,这个空间几何体的正视图可能是C。
知识点
如图放置的边长为2的正方形PABC沿




正确答案
4
解析
由于本题是求两个相邻零点问的图象与



知识点
已知向量




正确答案
解析
由







知识点
设两个向量




正确答案
解析
根据已知条件得









知识点
一个几何体的三视图如图所示,其正视图和侧视图都是底边长分别为2和4,腰长为4的等腰梯形,则该几何体的侧面积是
正确答案
解析
结合三视图可知该几何体是一个圆台,其上,下底面的半径分别为2,1,其直观图如图所示,则该几何的侧面积
知识点
由直线


正确答案
解析
由






知识点
扫码查看完整答案与解析