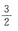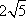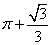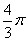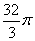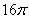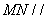- 立体几何与空间向量
- 共3353题
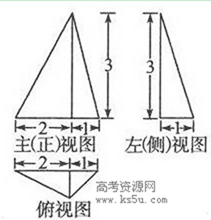
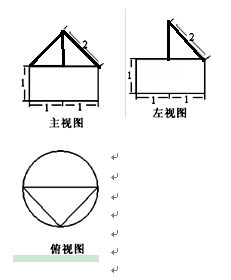
一个空间几何体的三视图如图所示，该几何体的体积为______.
正确答案
96
解析
略
知识点
已知某几何体的三视图如图所示，则该几何体的体积为 .
正确答案
解析
略
知识点
右上图是一个几何体的三视图，由图中数据可知该几何体中最长棱的长度是（ ）
A
B
C
D
正确答案
解析
略
知识点
图2是一个组合体的三视图，根据图中数据，可得该几何体的表面积等于（几何体的接触面积可忽略不计）
正确答案
解析
从三视图可以看出该几何体是由一个球和一个圆柱组合而成的，其表面及为
知识点
某几何体的三视图如图3所示，其正视图是边长为2的正方形，侧视图和俯视图都是等腰直角三角形，则此几何体的体积是 。
正确答案
解析
略
知识点
一个空间几何体的三视图如图所示，该几何体的体积为______.
正确答案
96
解析
略
知识点
已知某几何体的三视图如右图所示，则该几何体的体积是
A
B
C
D
正确答案
解析
略
知识点
已知一个几何体的三视图如图所示，则该几何体的体积（单位：cm3）为 _____________.
正确答案
解析
略
知识点
已知某几何体的三视图如图所示，则该几何体的体积为
正确答案
12
解析
略
知识点
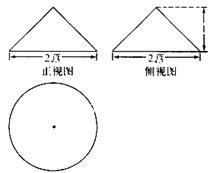
某几何体的三视图如图所示，则该几何体外接球的表面积为
A
B
C
D
正确答案
解析
略
知识点
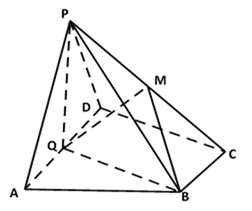
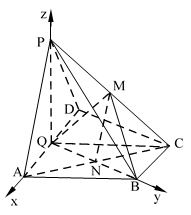
如图，在四棱锥
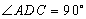
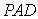
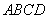
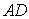
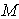
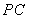
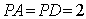
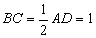
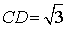
（1）若点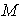
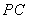
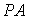
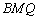
（2）若二面角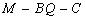
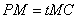
试确定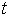
正确答案
见解析。
解析
（1）证明：连接
∵
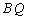
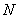
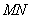
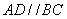
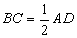
∴四边形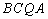
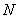
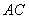
又∵点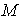
∴
∵
∴
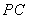
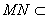
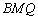
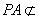
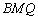
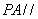
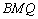
（2）解：∵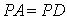
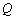
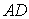
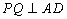
∵平面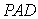
∴
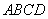
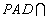
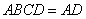
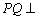
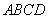
如图，以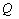
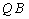
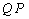
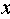
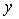
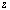
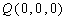
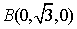
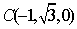
于是平面
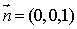
设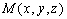
则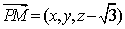
∵
∴ 
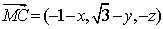
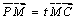
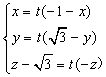
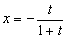
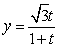
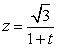
在平面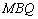
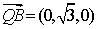
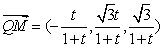
设平面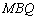
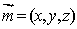
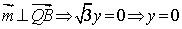
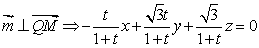
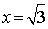
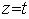
∴平面
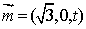
∵二面角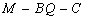
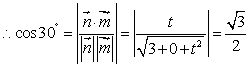
解得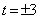
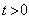
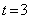
知识点
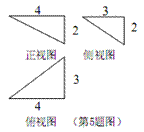
如图，一个空间几何体的主视图、左视图、俯视图为
全等的等腰直角三角形，如果
那么这个几何体的体积为 ( )
A1
B
C
D
正确答案
解析
可知该几何体是三棱锥，底面面积为
知识点
如图是一个正三棱柱的三视图，若三棱柱的体积是
正确答案
2
解析
略
知识点
一个几何体的正视图、侧视图、和俯视图形状都相同，大小均相等，则这个几何体不可以是
正确答案
解析
略
知识点
某几何体的三视图如图1所示，且该几何体的体积是
A2
B
C
D3
正确答案
解析
略
知识点
扫码查看完整答案与解析