- 立体几何与空间向量
- 共3353题
某四面体的三视图如下图所示,则该四面体的四个面中,直角三角形的面积和是_______.
正确答案
解析
由三视图可得原几何体如图,该几何体的高PO=2,底面ABC为边长为2的等腰直角三角形,所以在该几何体中,直角三角形是底面ABC和侧面PBC,事实上,∵PO⊥底面ABC,∴平面PAC⊥底面ABC,而BC⊥AC,∴BC⊥平面PAC,∴BC⊥PC。
所以

知识点
在平面直角坐标系xOy中,已知角α的顶点与点O重合,始边与x轴的非负半轴重合,终边上一点M的坐标为(

正确答案
解析
∵角α终边上一点M的坐标为(
∴sinα=

∴cos(α+


=

故选:B.
知识点
“直线l垂直于平面α”的一个必要不充分条件是( )
正确答案
解析
根据面面垂直的判定可知,直线l垂直于平面α,则经过直线l的某一个平面与平面α垂直,
当经过直线l的某一个平面与平面α垂直时,直线l垂直于平面α不一定成立,
∴“经过直线l的某一个平面与平面α垂直”是“直线l与平面α垂直”的必要不充分条件。
故选:D
知识点
采用系统抽样方法从1000人中抽取50人做问卷调查,为此将他们随机编号为1,2,…,1000,适当分组后在第一组采用简单随机抽样的方法抽到的号码为8.抽到的50人中,编号落入区间[1,400]的人做问卷A,编号落入区间[401,750]的人做问卷B,其余的人做问卷C,则抽到的人中,做问卷C的人数为( )
正确答案
解析
若采用系统抽样方法从1000人中抽取50人做问卷调查,则需要分为50组,每组20人,若第一组抽到的号码为8.,则以后每组抽取的号码分别为28,48,68,88,108,……,所以编号落入区间[1,400]的有20人,编号落入区间[401,750]的有18人,所以做问卷C的有12人。
知识点
在如图所示的几何体中,四边形










(1)求证:
(2)若二面角


正确答案
见解析。
解析
(1)证明:在
所以


又因为 


所以 
又因为



所以 
(2)因为




设






设平面


令

又平面

所以

所以

知识点
已知△EFH是边长为1的正三角形,动点G在平面EFH内,若


则

正确答案
解析
以EF的中点为坐标原点,EF所在直线为x轴,建立如图的直角坐标系,
则E(﹣


由|

即有﹣1≤x≤1①
又




由


即有x<﹣
由①②可得﹣1≤x<﹣
则


则所求范围为[﹣1,﹣
故选A.
知识点
如图,斜三棱柱





(1)求证:平面

(2)求证:
(3)求二面角
正确答案
见解析。
解析
(1)证明:设

在斜三棱柱








∴

∴






解法一:(2)连接










(3)过点










设











在



∴


∴二面角

解法二:(2)因为点













设

设


又


(3)设平面

则
∴

设平面

∴





知识点
如图,已知椭圆Γ:

椭圆Γ的左焦点和右顶点,且|AF|=3。
(1)求椭圆Γ的方程;
(2)过点F作一条直线l交椭圆Γ于P,Q两点,点Q关于x轴的对称点为Q'。
若PF∥AQ′,求证:|PF|=
正确答案
见解析。
解析
(1)设椭圆Γ的半焦距为c,则
(2)方法一:依题意得,PQ与坐标轴不垂直,设P(x1,y1),Q(x2,y2),由题意的对称性可得Q′(x2,﹣y2),由PF∥AQ',利用斜率相等可得



方法二:依题意得,PQ与坐标轴不垂直,设l方程为y=k(x+1)(k≠0),P(x1,y1),Q(x2,y2),可得Q′(x2,﹣y2),与椭圆的方程联立可得(3+4k2)x2+8k2x+4k2﹣12=0.可得根与系数的关系,由于PF∥AQ',可得直线AQ'的方程为y=k(x﹣2),与椭圆的方程联立可得(3+4k2)x2﹣16k2x+16k2﹣12=0.可得根与系数的关系,解出k及其点P,Q的坐标即可得出;
方法三:依题意,得PQ与坐标轴不垂直,设l方程为y=k(x+1)(k≠0),P(x1,y1),Q(x2,y2),可得Q′(x2,﹣y2),与椭圆方程联立可得(3+4k2)y2﹣6ky﹣9k2=0.得到根与系数的关系,由于PF∥AQ',可得直线AQ'的方程为y=k(x﹣2),与椭圆的方程联立可得(3+4k2)y2+12ky=0.可得


方法四:依题意,得PQ与坐标轴不垂直,设l方程为y=k(x+1)(k≠0),P(x1,y1),Q(x2,y2),可得Q′(x2,﹣y2),由于P,F,Q三点共线,
可得







方法五:依题意,得PQ与坐标轴不垂直,设l方程为y=k(x+1)(k≠0),P(x1,y1),Q(x2,y2),可得Q′(x2,﹣y2),直线PQ'过定点M(﹣4,0),理由如下:与椭圆方程联立可得:(3+4k2)x2+8k2x+4k2﹣12=0.

(1)设椭圆Γ的半焦距为c,则
解得a=2,c=1,
∴b2=a2﹣c2=3,
∴椭圆Γ的方程为
(2)方法一:依题意得,PQ与坐标轴不垂直,设P(x1,y1),Q(x2,y2)。
∵点Q与点Q′关于x轴对称,∴Q′(x2,﹣y2)。
由(1)讨论可知,A(2,0),F(﹣1,0)。
∵PF∥AQ',
∴直线FQ与直线AQ'的斜率相等,
故
解得
又∵点Q(x2,y2)在椭圆Γ上,
∴

由椭圆对称性,不妨取
则直线PQ的斜率
∴直线PQ方程为
联立

∴

∴
方法二:依题意得,PQ与坐标轴不垂直。
设l方程为y=k(x+1)(k≠0),P(x1,y1),Q(x2,y2)。
∵点Q与点Q′关于x轴对称,∴Q′(x2,﹣y2)。
又∵椭圆关于x轴对称,∴点Q′也在椭圆Γ上。
由
∴
∵PF∥AQ',∴直线AQ'的方程为y=k(x﹣2)。
由
∵直线AQ'交椭圆于A(2,0),Q'(x2,﹣y2)两点,
∴
故
∴
解得
∴
∴

∴
方法三:依题意,得PQ与坐标轴不垂直。
设l方程为y=k(x+1)(k≠0),P(x1,y1),Q(x2,y2)。
∵点Q与点Q′关于x轴对称,∴Q′(x2,﹣y2)。
又∵椭圆关于x轴对称,∴点Q′也在椭圆Γ上。
由
∴
∵PF∥AQ',∴直线AQ'的方程为y=k(x﹣2)。
由
∵直线AQ'交椭圆于A(2,0),Q'(x2,﹣y2)两点,
∴

设
∴
∴

∴

方法四:依题意,得PQ与坐标轴不垂直。
设l方程为y=k(x+1)(k≠0),P(x1,y1),Q(x2,y2)。
∵点Q与点Q′关于x轴对称,∴Q′(x2,﹣y2)。
∵P,F,Q三点共线,
∴

∴(x1+1)y2﹣(x2+1)y1=0。
∵PF∥AQ',∴可设
∴x1+1=λ(x2﹣2),y1=﹣λy2。
∴λ(x2﹣2)y2+λ(x2+1)y2=0,即λy2(2x2﹣1)=0。
依题意,y1•y2≠0,∴
∵点


解得

由椭圆对称性,不妨取
则

∵点

∴

∴

方法五:依题意,得PQ与坐标轴不垂直。
设l方程为y=k(x+1)(k≠0),P(x1,y1),Q(x2,y2)。
∵点Q与点Q′关于x轴对称,∴Q′(x2,﹣y2)。
直线PQ'过定点M(﹣4,0),理由如下:
由
∴
∴

∵
∴
∴
∴M,P,Q'三点共线,即直线PQ'过定点M(﹣4,0),
∵F为线段AM中点,PF∥AQ',∴
知识点
如图,在四棱锥







(1)求证:平面

(2)若直线



正确答案
解析
(1)∵平面

平面

∴
又∵
由已知




∴

∴

∴

∴

∴平面

(2)由(1),平面

设直线


∴
∵
∴

设平面


由
∴


∴

显然二面角
∴二面角
知识点
已知一个空间几何体的直观图和三视图(尺寸如图所示)。
(1)设点M为棱PD中点,求证:EM∥平面ABCD;
(2)线段PD上是否存在一点N,使得直线BN与平面PCD所成角的正弦值等于
正确答案
见解析。
解析
(1)以B为原点,


(2)求出平面PCD的法向量和平面PCD的一个法向量,由此利用向量法能求出线段PD上存在一点N,当N点与D点重合时,直线BN与平面PCD所成角的正弦值等于
(1)证明:由三视图知,BA,BP,BC两两垂直,故以B为原点,



建立如图所示的空间直角坐标系,…(1分)
则P(0,2,0),D(2,0,1),M(1,1,
所以

平面ABCD的一个法向量等于
所以

又EM⊄平面ABCD,所以EM∥平面ABCD.(5分)
(2)解:当点N与点D重合时,直线BN与平面PCD所成角的正弦值为
理由如下:
因为


由
取y=1,得平面PCD的一个法向量
假设线段PD上存在一点N,使得直线BN与平面PCD所成角α的正弦值等于
设

则

所以sinα=|cos<

=
=

所以9λ2﹣8λ﹣1=0,解得λ=1,或
因此,线段PD上存在一点N,当N点与D点重合时,
直线BN与平面PCD所成角的正弦值等于
知识点
已知函数
(1)求函数
(2)在




正确答案
见解析
解析
(1)∵
=

∴函数
(2)∵

又

∴
在

∴

∴
∴
知识点
如图,三棱柱






(1)求证:

(2)求锐二面角
正确答案
见解析
解析
(1)连结



∴
又

∴面

∴


设

∴

又


(2)以


设
则


由(1)知,

∴可取平面

设平面

由
∴可取
设锐二面角

则
∴所求锐二面角

知识点
4.某几何体的三视图如下图所示,则该几何体的表面积为( )
正确答案
解析
由三视图可知几何体为下部是底面半径为3,高为6的圆柱,上部是侧棱长为5,底面边长为





知识点
9.在平面直角坐标系xoy中,以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,已知直线l的极坐标方程为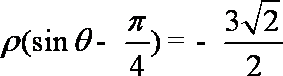
正确答案

解析
由题意可知,直线l: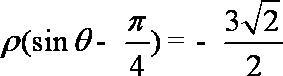
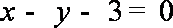
知识点
11.已知向量



正确答案
3
解析
因为







知识点
扫码查看完整答案与解析




































































