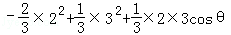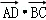- 立体几何与空间向量
- 共3353题
如图，在长方体
（1）求证：D1E⊥A1D；
（2）求AB的长度；
（3）在线段AB上是否存在点E，使得二面角
点E的位置；若不存在，请说明理由。
正确答案
见解析。
解析
（1）证明：
连结AD1，由长方体的性质可知：
AE⊥平面AD1，∴AD1是ED1在
平面AD1内的射影。又∵AD=AA1=1，
∴AD1⊥A1D
∴D1E⊥A1D1（三垂线定理）
（2）设AB=x，∵四边形ADD1A是正方形，
∴小蚂蚁从点A沿长方体的表面爬到
点C1可能有两种途径，如图甲的最短路程为
如图乙的最短路程为
（3）假设存在，平面DEC的法向量
设平面D1EC的法向量
由题意得：
解得：
知识点
某简单组合体的三视图如图2，其中正视图与侧视图相同（尺寸如图，单位：cm），则该组合体的体积是 
正确答案
解析
略
知识点
如图是一个几何体的三视图，根据图中数据，可得该几何体的表面积、体积分别是（ ）
A32π、
B16π、
C12π、
D8π、
正确答案
解析
三视图复原的几何体是半径为2的半球，
所以半球的表面积为半个球的表面积与底面积的和：2πr2+πr2=3πr2=12π。
半球的体积为：
故选C。
知识点
如图，一个空间几何体的主视图和左视图都是边长为1的正三角形，俯视图是一个圆，那么几何体的侧面积为
A
B
C
D
正确答案
解析
略
知识点
已知某几何体的三视图如图所示，则该几何体的体积为 （） .
正确答案
解析
略
知识点
在
正确答案
解析
略
知识点
如图是一个几何体的三视图，若它的体积是3
A
B
C
D
正确答案
解析
由三视图可知此几何体为一个三棱柱，其直观图如图：底面三角形ABC为底边AB边长为2的三角形，AB边上的高为AM=a，侧棱AD⊥底面ABC，AD=3，
∴三棱柱ABC﹣DEF的体积V=S△ABC×AD=
∴a=
故选C。
知识点
在△ABC中，∠BAC=90º，D是BC中点，AB=4，AC=3，则
A
B
C
D7
正确答案
解析
略
知识点
坐标系与参数方程选做题）在极坐标系
正确答案
解析
略
知识点
已知向量
正确答案
-3
解析
略
知识点
已知在三角形ABC中，AB=2，AC=3，∠BAC=θ，若D为BC的三等分点〔靠近点B一侧），则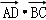
正确答案
（﹣
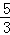
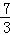
解析
解：∵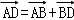
∴
=
=
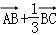
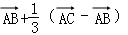
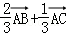
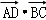
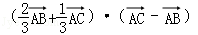
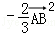
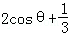
∵﹣1＜cosθ＜1，∴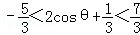
∴
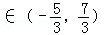
故答案为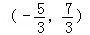
知识点
若一个底面是正三角形的三棱柱的正视图如图所示,则其表面积等于
正确答案
解析
略
知识点
已知
A
B
C
D
正确答案
解析
略
知识点
某几何体的三视图如图所示，则它的体积是（ ）
A
B
C
D
正确答案
解析
略
知识点
已知三边长分别为4.5.6的△ABC的外接圆恰好是球O的一个大圆，P为球面上一点，若点P到△ABC的三个顶点的距离相等，则三棱锥P—ABC的体积为
正确答案
10
解析
略
知识点
扫码查看完整答案与解析