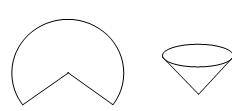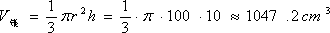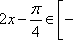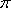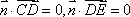- 立体几何与空间向量
- 共3353题
已知向量


正确答案
解析
知识点
已知一个几何体的三视图及其大小如图,这个几何体的体积V=( )
正确答案
解析
由几何体的三视图知这个几何体是一个下面是圆柱,上面是圆锥的简单几何体.
圆柱底面直径为4,高为3,圆锥高为3,
知识点
某建筑物的上半部分是多面体MN—ABCD,下半部分是长方体ABCD—A1B1C1D1(如图4),该建筑物的正(主)视图和侧(左)视图如图5,其中正(主)视图由正方形和等腰梯形组合而成,侧(左)视图由长方形和等腰三角形组合而成。
(1)求直线AM与平面A1B1C1D1所成角的正弦值;
(2)求二面角A—MN—C的余弦值;
(3)求该建筑物的体积。
正确答案
见解析
解析
(1)作MO⊥平面ABCD,垂足为O,连接AO,
则∠MAO是直线AM与平面ABCD所成的角,
由于平面ABCD∥平面A1B1C1D1,
故∠MAO是直线AM与平面A1B1C1D1所成的角,
作MP⊥AB,垂足为P,连接PO,

∴MO⊥AB。


∴AB⊥平面MOP,
由题意知
在
在
在
∴直线


(2)延长PO交CD于点Q,连接MQ,
由(1)知AB⊥平面MOP
∴MQ
∴AB⊥MQ。
∵MN∥AB,
∴MN⊥MP,MN⊥MQ,
∴∠PMQ是二面角A一MN—C的平面角,
在△PMQ中,

∴二面角A一MN一C的余弦值为0.
(3)作NP1∥MP交AB于点P1,作NQ1 ∥MQ交CD于点Q1,
由题意知多面体MN—ABCD可分割为两个等体积的四棱锥M—APQD和
和一个直三棱柱
四棱锥

直三棱柱
∴多面体

长方体
∴建筑物的体积为
解法2:
(1)以点D为原点,DA所在直线为


建立空间直角坐标系
作OP⊥AB,垂足为P,依题意知
则


∴平面
设直线

则
∴直线


(2)由(1)知
设平面
由
令
∴平面

设平面
由
令
∴平面CDMN的一个法向量为
∴平面ABNM⊥平面CDMN,
∴二而角A一MN一C的余弦值为0.
(3)如图将多面体
依题意知
多面体

棱锥

∴直三棱柱
三棱锥
∴多面体

长方体

∴建筑物的体积为
知识点
如图,四棱锥P﹣ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点。
(1)求证:CD⊥AE;
(2)求证:PD⊥面ABE;
(3)求二面角A﹣PD﹣C的平面角的正弦值。
正确答案
见解析。
解析
解:(1)证明:PA⊥底面ABCD,∴CD⊥PA。
又CD⊥AC,PA∩AC=A,故CD⊥面PAC,AE⊆面PAC,故CD⊥AE。
(2)证明:PA=AB=BC,∠ABC=60°,故PA=AC,E是PC的中点,故AE⊥PC,
由(1)知CD⊥AE,从而AE⊥面PCD,故AE⊥PD,易知BA⊥PD,故PD⊥面ABE。
(3)过点A作AF⊥PD,垂足为F,连接EF。
由(2)知,AE⊥面PCD,故∠AFE是二面角A﹣PD﹣C的一个平面角。
设AC=a,则


从而

知识点
从一个正方体中截去部分几何体,得到的几何体的三视图及尺
寸(单位:cm)如图1所示,则此几何体的体积是
正确答案
解析
该几何体的直观图如右图示:其体积
知识点
已知




正确答案

解析
解析:由题意知

∴最小正周期 

当



当


知识点
如图,已知正四棱柱





(1)求直线

(2)求过

正确答案
(1)
解析
(1)连结






连结











(2)









知识点
若某几何体的三视图(单位:cm)如图所示,则此几何体的体积是() 
正确答案
6
解析
几何体如图所示,正面为



知识点
已知


正确答案
解析
略
知识点
已知四棱锥P-ABCD的三视图如下图所示,E是侧棱PC上的动点。
(1)求四棱锥P-ABCD的体积;
(2)是否不论点E在何位置,都有BD⊥AE?证明你的结论;
(3)若点E为PC的中点,求二面角D-AE-B的大小。
正确答案
见解析。
解析
(1)由三视图可知,四棱锥P-ABCD的底面是边长为1的正方形,
侧棱PC⊥底面ABCD,且PC=2.
∴
(2)不论点E在何位置,都有BD⊥AE.
证明如下:连结AC,∵ABCD是正方形,∴BD⊥AC.
∵PC⊥底面ABCD,且BD⊂平面ABCD,∴BD⊥PC.
又∵AC∩PC=C,∴BD⊥平面PAC.
∵不论点E在何位置,都有AE⊂平面PAC.
∴不论点E在何位置,都有BD⊥AE.
(3)解法1:在平面DAE内过点D作DF⊥AE于F,连结BF.
∵AD=AB=1,
∴Rt△ADE≌Rt△ABE,
从而△ADF≌△ABF,∴BF⊥AE.
∴∠DFB为二面角D-AE-B的平面角。
在Rt△ADE中,
又BD=
cos∠DFB=
∴∠DFB=
即二面角D-AE-B的大小为
解法2:
如图,以点C为原点,CD,CB,CP所在的直线分别为x,y,z轴建立空间直角坐标系,则D(1,0,0),A(1,1,0),B(0,1,0),E(0,0,1),
设平面ADE和平面ABE的法向量分别为

由
由
设二面角D-AE-B的平面角为θ,则
∴θ=

知识点
如图,用半径为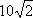
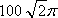
正确答案
见解析
解析
设铁皮扇形的半径和弧长分别为R、l,圆锥形容器的高和底面半径分别为h、r,则由题意得R=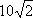
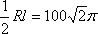
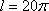
由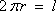
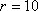
由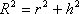
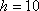
由
所以该容器最多盛水1047.2cm3 ………………………12分
(说明:
知识点
已知向量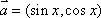
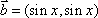
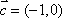
(1)若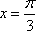
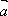
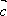
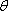
(2)若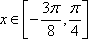
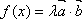

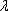
正确答案
见解析
解析
(1)当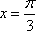
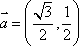
所以 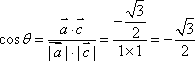
因而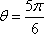
(2)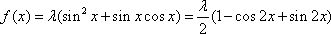
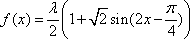
因为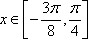
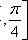
当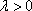
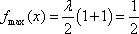
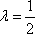
当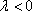
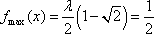
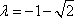
所以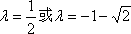
知识点
已知长方体的一个顶点上的三条棱长分别是
正确答案
解析
因为球的半径为R=

为
知识点
已知向量



且

(1)求

(2)若


正确答案
见解析。
解析
(1)

∴





(2)由(1)可得
∵ 


∴当


当

∴

知识点
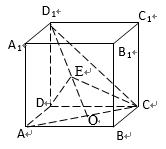
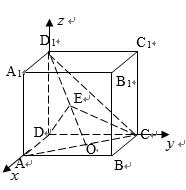
如图:在正方体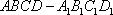

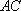
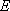
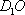
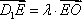
(1)求证: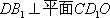
(2)若平面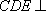
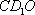
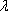
正确答案
见解析
解析
(1)不妨设正方体的棱长为1,如图建立空间直角坐标系,
则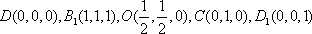
于是: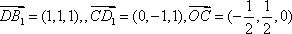
因为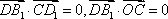
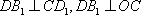
故: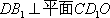
(2)由(1)可知平面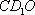
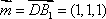
由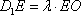
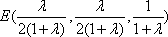
又设平面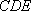
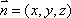
得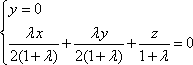
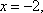
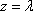
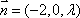
因为平面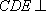
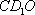
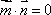
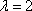
知识点
扫码查看完整答案与解析