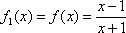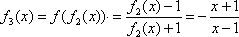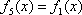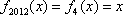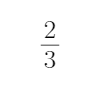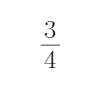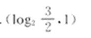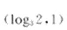- 函数的值
- 共96题
已知函数y=f(x)是奇函数,当x>0时,f(x)=log2x,则f(f(
正确答案
-1
解析
解:∵y=f(x)是奇函数,
∴f(﹣x)=﹣f(x)
∵当x>0时,f(x)=log2x,
∴
则f(f(
故答案为:﹣1
知识点
设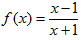
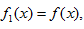
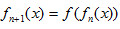
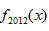
正确答案
x
解析
由题目可预知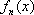
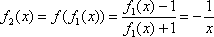
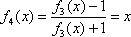
……,可知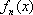
知识点
设集合A

正确答案
解析
略
知识点
函数f(x)对任意x∈R,都有f(x+6)+f(x)=2f(3),y=f(x﹣1)图象关于点(1,0)对称,f(4)=4,则f(2012)= 。
正确答案
-4
解析
由f(x+6)+f(x)=2f(3),得f(x+12)+f(x+6)=2f(3),
两式相减,得f(x+12)﹣f(x)=0,即f(x+12)=f(x),
∴12为函数y=f(x)的周期,
由y=f(x﹣1)的图象关于点(1,0)对称,知y=f(x)的图象关于(0,0)对称,
∴f(x)是奇函数,
由f(x+6)+f(x)=2f(3),令x=﹣3,得f(3)=f(﹣3),
∴f(3)=f(﹣3)=0,即f(x+6)+f(x)=0,
∴f(x+6)=﹣f(x),
∴f(2012)=f(2012﹣12×167)=f(8)=﹣f(2)=f(﹣2)=﹣f(4)=﹣4,
故答案为:﹣4。
知识点
9. 已知函数
正确答案
0
解析
解析已在路上飞奔,马上就到!
知识点
12.设

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.已知奇函数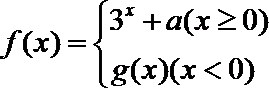
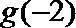
正确答案
-8
解析
解析已在路上飞奔,马上就到!
知识点
8.已知f(x)是定义在R上的函数,f(1)=10,且对于任意x∈R都有f(x+20)≥f(x)+20,f(x+1)≤f(x)+1,若g(x)=f(x)+1-x,则g(10)=( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.设







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.已知函数
(1)求
(2)画出函数
(3)若关于x 的方程

正确答案
(1)
(2)单调增区间为

(3)
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析