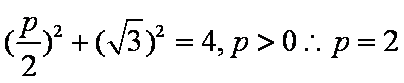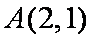- 直线与圆的位置关系
- 共93题
已知曲线C1:


(1)指出C1,C2各是什么曲线,并说明C1与C2公共点的个数;
(2)若把C1,C2上各点的纵坐标都压缩为原来的一半,分别得到曲线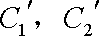
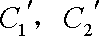
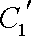
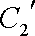
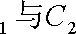
正确答案
见解析
解析
(1)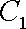
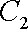
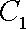
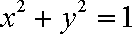
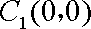
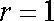
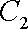
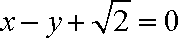
因为圆心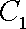
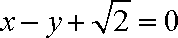

所以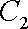
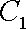
(2)压缩后的参数方程分别为
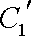


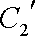
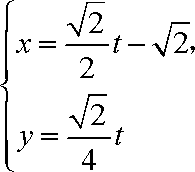
化为普通方程为: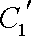

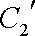
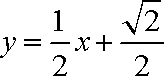
联立消元得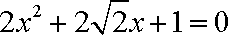
其判别式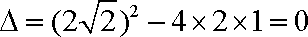
所以压缩后的直线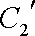
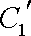
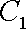
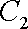
知识点
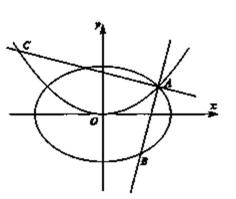
已知椭圆的中心在原点,焦点在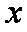

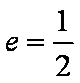
(1)求椭圆的方程;
(2)椭圆的左、右顶点分别为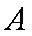
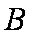
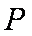
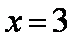
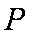
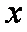
连结


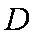
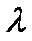
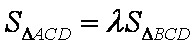
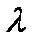
正确答案
见解析
解析
(1)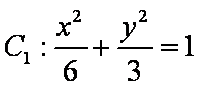

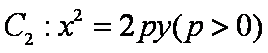

由条件得
所以抛物线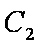
(2)由
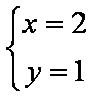
设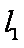
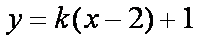
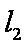
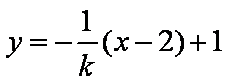
设
将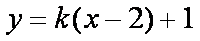
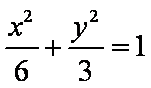
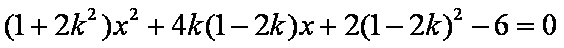
由韦达定理得: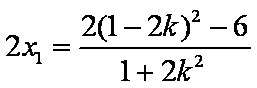
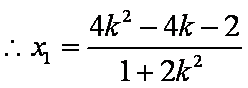
同理,将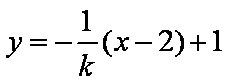


由韦达定理得: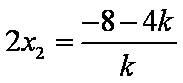

所以
因为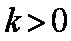
知识点
在极坐标系中,圆



正确答案
解析
直线的方程为x=2,圆的方程为
知识点
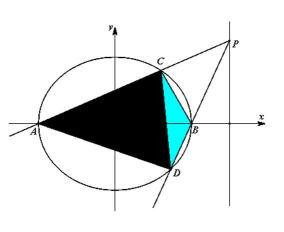
如图,已知直线




(1)求

(2)设











(3)在(2)的条件下,记点










正确答案
见解析
解析
(1)由已知,圆


由题设圆心到直线


解得

设




代入直线方程得:
∴

(2)由(1)知抛物线


设



令

所以

∴
∴


(3)设直线
得



则
∴
∵
∴


知识点
已知圆








(1)求点

(2)过点










正确答案
(1)
(2)
解析
(1)设


由题可知:

而

故点

(2)当直线



当直线



设





∴
同理可设





∴
故
综上可知:

知识点
扫码查看完整答案与解析