- 函数单调性的判断与证明
- 共139题
1
题型:
单选题
|
设函数
正确答案
D
解析
略
知识点
函数单调性的判断与证明
1
题型:
单选题
|
“函数



正确答案
A
解析
略
知识点
充要条件的判定函数单调性的判断与证明
1
题型:
单选题
|

则
正确答案
D
解析
略
知识点
函数单调性的判断与证明
1
题型:填空题
|
有甲、乙、丙在内的6个人排成一排照相,其中甲和乙必须相邻,丙不排在两头,则这样的排法共有()种。
正确答案
144
解析
略
知识点
函数单调性的判断与证明
1
题型:简答题
|
已知函数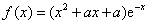
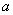
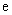
(1)当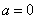
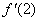
(2)若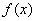
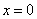
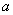
(3)在(2)的条件下,设由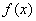
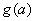
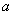
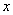
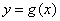
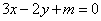
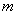
正确答案
见解析
解析
(1)当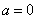
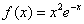
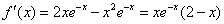
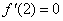
(2)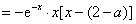
令
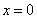
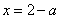
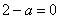
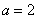

此时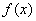
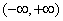
当
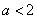
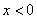
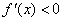
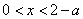
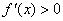
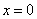
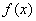
当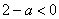
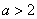
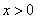
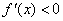
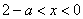
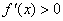

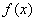
综上所述,使函数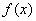
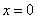
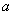
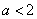
(3)由(2)知当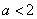


因此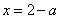

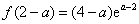
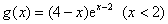
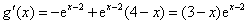
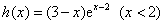
则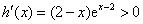
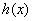
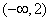
所以当
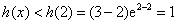
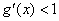
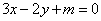
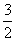
所以曲线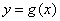
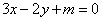
知识点
函数单调性的判断与证明
下一知识点 : 函数单调性的性质
扫码查看完整答案与解析