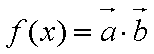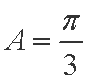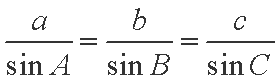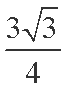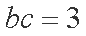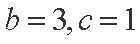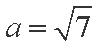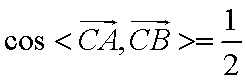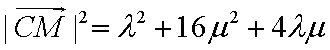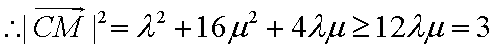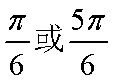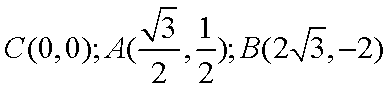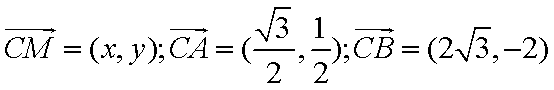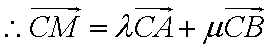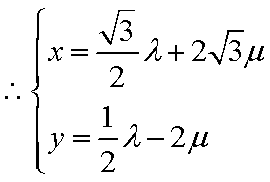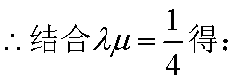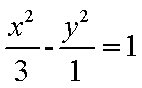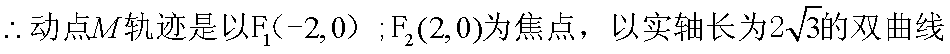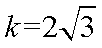- 函数单调性的判断与证明
- 共139题
1
题型:简答题
|
如图,已知四棱锥






(1)证明

(2)求二面角
正确答案
见解析
解析
解法一:(1)连结




∵底面ABCD是正方形,∴



∴






解法二:(1))以


设

∴


则由
∵


(2) 由(1)知





∴
知识点
函数单调性的判断与证明
1
题型:简答题
|
已知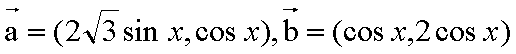
(1)若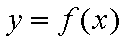

(2)在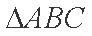
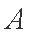
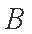

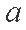
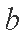

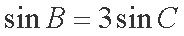
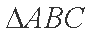
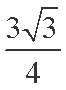

正确答案
见解析。
解析
(1)

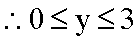
(2)∵ f(A)= 2 ∴
∴ 
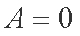
∵ 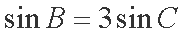
∴ 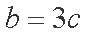
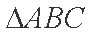
∴ 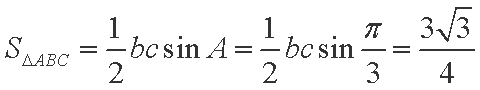
由①和②解得
∵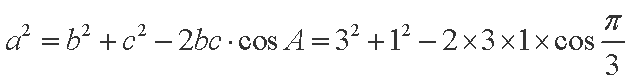
知识点
函数单调性的判断与证明
1
题型:简答题
|
已知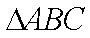
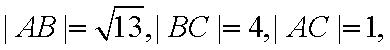
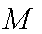
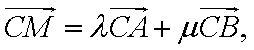
(1)求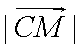
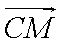

(2)是否存在两定点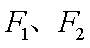
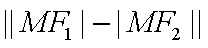
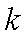
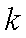
正确答案
见解析。
解析
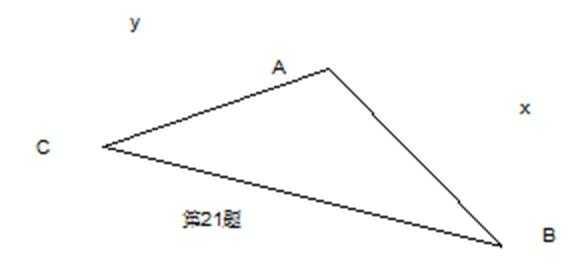
(1)由余弦定理得:
将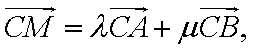

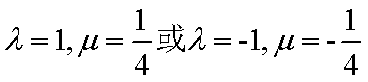
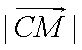
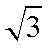
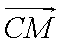
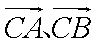
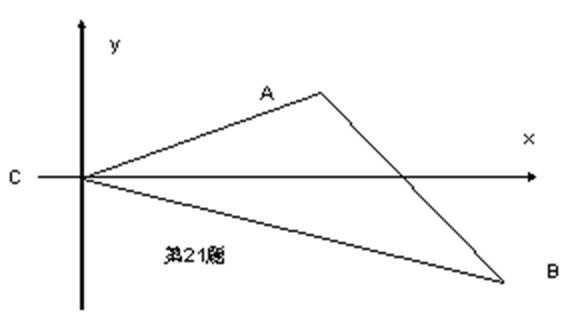
(2)
以顶点C为坐标原点,以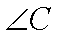

设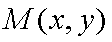

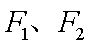
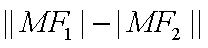
知识点
函数单调性的判断与证明
1
题型:填空题
|
16.将正奇数





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
函数单调性的判断与证明
1
题型:
单选题
|
5. 下列函数中,在
正确答案
D
解析
解析已在路上飞奔,马上就到!
知识点
函数单调性的判断与证明函数零点的判断和求解
下一知识点 : 函数单调性的性质
扫码查看完整答案与解析