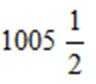- 等比数列
- 共414题
10.如图所示是毕达哥拉斯的生长程序:正方形上连接着一个等腰直角三角形,等腰直角三角形的直角边上再连接正方形

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.正项等比数列{an}中,存在两项am、an使得

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
22.对于函数








(1)判断函数
(2)已知







(3)在(2)的条件下,试比较

正确答案
(1)
∴
∴ 是“幅度函数”,其“幅度”为2
(2)
∵ 


∴ 当
当
∴ 
∴
(3)
令

∴
∴ 
解析
解析已在路上飞奔,马上就到!
知识点
17.已知等差数列
(1)求数列
(2)设各项均为正数的等比数列

正确答案
(1)设等差数列
∴数列
(2)设各项均为正数的等比数列
由(1)知

解析
解析已在路上飞奔,马上就到!
知识点
18.若数列

(1)若数列


(2)若数列

(3)若



(4)若


其中,错误命题的序号是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15. 已知函数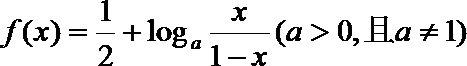
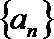
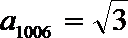
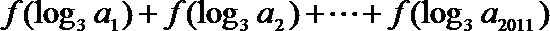
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2. 由正数组成的等比数列{an}中,a1+a2=1,a3+a4=4,则a5+a6=( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.数列{an}中a1=1,a5=13,an+2+an=2an+1;数列{bn}中,b2=6,b3=3,bn+2bn=

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
22.
64个正数排成8行8列, 如上图所示:在符合



(1)若


(2)记第n行各项之和为An(1≤n≤8),数列{an}、{bn}、{cn}满足




(3)对(2)中的



正确答案
(1)∵
∴
∵
∴
(2)设第一行公差为d,
解出:

∵
∴
∴
∵
∴
而
∴
∴
故
∵
∴
∴
(3)∵
∴
∴
解出:6.643<n≤7.643
∵
∴n=7,即
解析
解析已在路上飞奔,马上就到!
知识点
22.若



(1)求数列
(2)设集合





(3)







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析