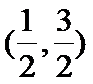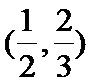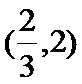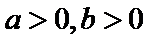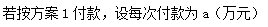等比数列
共414题

等比数列
共414题

热门试卷

X 查看更多试卷

题型：简答题

简答题 · 9 分

26．设二次方程有两根和，且满足．

（1）试用表示；

（2）求证：是等比数列；

（3）当时，求数列的通项公式．

正确答案

（1）根据韦达定理得，由得

故

（2）因为，所以

所以数列是等比数列

（3）当的首项为

所以所以：

解析

解析已在路上飞奔，马上就到！

知识点

由递推关系式求数列的通项公式等比数列的基本运算等比数列的判断与证明

题型：单选题

单选题 · 5 分

9．已知各项均为正数的等比数列满足,若存在两项使得的最小值为（　　）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

等比数列的基本运算等比数列的性质及应用利用基本不等式求最值

题型：填空题

填空题 · 5 分

13．各项均为正数的等比数列{an}的前n项和为Sn，a1=1，a2•a4=16则S4=_________

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

等比数列的基本运算等比数列的性质及应用

题型：单选题

单选题 · 5 分

3.等比数列的前项和为，则公比等于( )

C或

D或

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

等比数列的基本运算

题型：单选题

单选题 · 5 分

3．已知等差数列的公差为2，若成等比数列，则等于（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

等差数列的基本运算等比数列的基本运算

题型：填空题

填空题 · 4 分

9．已知等比数列的公比不为1，其前项和为，若向量，，满足，则___________．

正确答案

121

解析

解析已在路上飞奔，马上就到！

知识点

平面向量数量积的运算量积判断两个平面向量的垂直关系等比数列的基本运算等比数列的性质及应用数列与向量的综合

题型：单选题

单选题 · 6 分

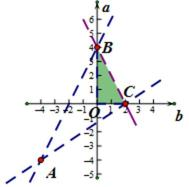
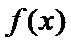
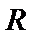
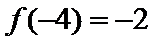
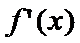
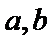
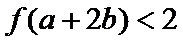
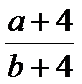
10．已知是定义域为的奇函数，,的导函数的图象如图所示，若两正数满足，则的取值范围是（）

正确答案

解析

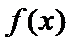
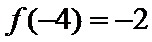
因为是定义域为的奇函数，，

所以，

由导函数的图象可知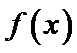在定义域上单调递增，

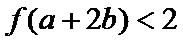
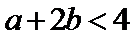
由得，，又

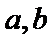
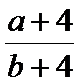
根据满足的条件画出可行域如图,

看作，与两点的直线斜率，

而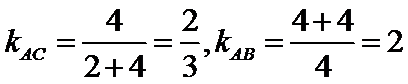,故，选C.

知识点

等比数列的基本运算

题型：简答题

简答题 · 12 分

20．某汽车销售公司为促销采取了较灵活的付款方式，对购买10万元一辆的轿车在一年内将款全部付清的前提下，可以选择以下两种分期付款方案购车：

方案1：分3次付清，购买后4个月第一次付款，再过4个月第二次付款，再过4个月第三次付款．

方案2：分12次付清，购买后1个月第一次付款，再过1个月第二次付款，……购买后12个月第十二次付款。

现规定分期付款中，每期付款额相同，月利率为0.8%，每月利息按复利计息，试比较以上两种方案的哪一种方案付款总数较少？（参考数据：1.0083=1.024，1.0084=1.033，1.00811=1.092，1.00812=1.1）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数模型的选择与应用等比数列的基本运算

题型：简答题

简答题 · 12 分

18．设各项均为正数的数列的前项和为，满足且恰好是等比数列的前三项．

（1）求数列、的通项公式；

（2）记数列的前项和为,若对任意的，恒成立，求实数的取值范围．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

由an与Sn的关系求通项an等比数列的基本运算等比数列的性质及应用数列与不等式的综合

题型：单选题

单选题 · 5 分

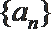
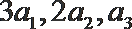
9.已知公比不为1的等比数列的首项为1，若成等差数列，则数列的前5项和为( )

C121

D31

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

等差数列的基本运算等差数列的性质及应用等比数列的基本运算等比数列的判断与证明等比数列的性质及应用

继续学习学习下一知识点

下一知识点 : 数列求和、数列的综合应用

百度题库 > 高考 > 理科数学 > 等比数列

扫码查看完整答案与解析