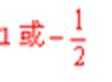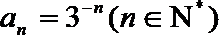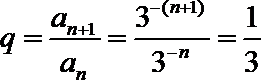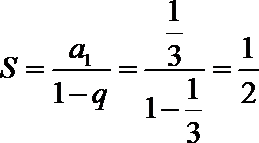- 等比数列
- 共414题
11.已知数列是公比为q的等比数列,且a2,a4,a3成等差数列,则q=______
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.已知数列
(1)求
(2)证明:对任意的
正确答案
(1)
∴ 
又 ∵
∴ 


∴
∴
(2) 由 (1) 知
∴ 原不等式成立
解析
解析已在路上飞奔,马上就到!
知识点
3.设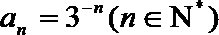
正确答案
解析
∵
∴首项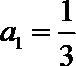
∴数列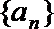
考查方向
本题主要考查无穷等比数列各项和公式,考查学生基础知识的掌握能力,是容易题.
解题思路
先求出数列的首项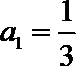
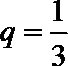
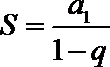
.
易错点
没注意到这是无穷等比数列,其公比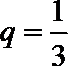
知识点
22.一个弹性小球从10米自由落下,着地后反弹到原来高度的

正确答案
解析
由an=10(

考查方向
本题主要考查等比数列求和
解题思路
1、求出an;
2、利用Sn的公式求解,即可得到结果。
A选项不正确,B选项不正确,D选项不正确,所以选C选项。
易错点
本题易在求和时发生错误。
知识点
32.已知两个无穷数列






(1)若数列

(2)若数列





①若数列

②若数列






正确答案
an=2n-1; 



解析
(1)数列


∴

(2)①∵数列



∴数列

故
② ∵

而数列



假设存在正整数





i.当
当



ii.当
显然不存在

iii.当
当


所以
当




此时



考查方向
本题主要考查数列的综合运算
解题思路
1、求出an,bn;
2、利用定义求解,即可得到结果。
易错点
本题易在利用新定义求解时发生错误。
知识点
5.等比数列


正确答案
解析
等比数列中,
所以

考查方向
解题思路
利用等比数列项和项数的关系,进而求解
易错点
利用等比数列前N项和公式求解,找a1和公比q,使试题复杂。
知识点
4.已知公比为




正确答案
解析
由等比数列的性质得:
又因为
所以


所以
考查方向
解题思路
1、先利用等比数列的性质得
2、仍然利用等比数列的性质得
易错点
1、忽略题中角标之间的关系导致无法解出答案;
2、对于性质:若

知识点
17.设{an}是公比大于1的等比数列,Sn为数列{an}的前n项和.已知S3=7且a1+3,3a2,a3+4构成等差数列.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)令bn=lnan,n=1,2,…,求数列{bn}的前n项和Tn.
正确答案
(Ⅰ)
(Ⅱ)
解析
(I)设{an}是公比q大于1的等比数列,∵a1+3,3a2,a3+4构成等差数列,
∴6a2=a3+4+a1+3,化为6a1q=
联立解得a1=1,q=2.∴an=2n﹣1.
(II)bn=lnan=(n﹣1)ln2,∴数列{bn}的前n项和Tn=
考查方向
解题思路
(Ⅰ)由于






(Ⅱ)把第(Ⅰ)问求得



易错点
本题在第二问构造中易出现错误
知识点
5.等比数列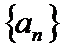
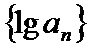
正确答案
解析
解:∵等比数列{an}中,a4=2,a7=5,
∴a1a10=a2a9=…=a4a7=10,
∴数列{lgan}的前10项和S=lga1+lga2+…+lga10
=lga1a2…a10=lg105=5.
故选:C.
考查方向
等比数列的前n项和.
解题思路
由等比数列的性质和对数的运算可得S=lga1a2…a10=lg105,化简可得.
易错点
利用对数的运算性质将等比数列转化为等差数列时,容易出错.
教师点评
本题考查等比数列的性质和求和公式,涉及对数的运算,属基础题.
知识点
8.Sn为等比数列{an}的前n项和,满足al=l,
正确答案
解析
因为





考查方向
解题思路
因为




易错点
不能正确排除干扰选项-3和-2。
知识点
扫码查看完整答案与解析