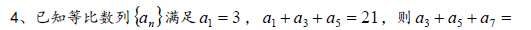等比数列_章节学习

1

题型：填空题

|

填空题 · 5 分

14．我们知道，把所有的正整数按照不同的方式排列，就会出现很多不同的意义。现在把所有正整数按从小到大的顺序排成如图所示的数表，其中第行共有个正整数，设表示位于这个数表中从上往下数第行，从左往右数第个数，若，则的和为．

正确答案

1004

解析

最后一个数是首项为1，等比为2的前n项和，n+1表示行数，当n=10时，即第11行的最后一个数为2047，第11行共有=1024个数，2047-2016=31,1024-31=993，即2016是第11行，第993个数，11+993=1004

考查方向

等比数列前n项和公式。

解题思路

最后一个数是首项为1，等比为2的前n项和，n+1表示行数，当n=10时，即第11行的最后一个数为2047，第11行共有=1024个数，2047-2016=31,1024-31=993，即2016是第11行，第993个数，11+993=1004

易错点

找不到规律；推理出错，计算错误都是导致出错的原因。

知识点

等差数列的基本运算等比数列的基本运算归纳推理

1

题型：单选题

|

单选题 · 5 分

5.已等比数列中,若, 则（）

A

B

C

D

正确答案

B

解析

由题得，

考查方向

该题主要考察了等比数列性质，该题属于简单题

解题思路

分别看做两个整体，将第一个整体看做首项，并找到两个整体项的公比

易错点

主要体现在不能将数列的连续两项看作整体

知识点

等比数列的基本运算等比数列的性质及应用

1

题型：填空题

|

填空题 · 5 分

13．已知等比数列为递增数列，其前n项和为，若，则公比q=__________.

正确答案

2

解析

考查方向

该题主要考察数列的通项公式及其前n项和公式运算，主要考察了定积分的运算

解题思路

该题思路比较简单直接

易错点

本题注意定积分计算易出错，公比求的两个结果都保留

知识点

定积分的计算等比数列的基本运算

1

题型：单选题

|

单选题 · 5 分

7．在等比数列{an）中，al=1，公比|q|≠1，若am=a2a5a10，则m=（　　）

A15

B16

C17

D18

正确答案

A

解析

在等比数列{an}中，由al=1，am=a2a5a10，

得，

又，∴m﹣1=14，即m=15．

故选A．

考查方向

本题主要考查等比数列的相关知识与性质，意在考查考生的运算求解能力及等比数列通项的应用能力，在近几年的各省高考题出现的频率较高，较易。

解题思路

利用al=1化简am=a2a5a10为即可。

易错点

本题只要能灵活al=1化简am=a2a5a10即可。

知识点

等比数列的基本运算

1

题型：简答题

|

简答题 · 12 分

17．在等比数列中，．(Ⅰ)求数列的通项公式；(Ⅱ)设，且为递增数列，若，求证：．

正确答案

（1）时，；时，

（2）由题意知：

∴

解析

（1）具体的分析如下：时，；时，

（2）由题意知：

∴∴

∴

考查方向

等比数列的通项公式，裂项相消法求和．

解题思路

先求出bn，然后用裂项相消求和

易错点

分类讨论p=1和p不等1时候的情况

知识点

由数列的前几项求通项等比数列的基本运算数列与不等式的综合

1

题型：单选题

|

单选题 · 5 分

3.在各项均为正数的等比数列{an}中，若am+1 • am-1 = am2 (m(m≥2)，数列{an}的前n项积为Tn，若T2m-1=512,则m的值为（）

A4

B5

C6

D7

正确答案

B

解析

设，，，

，数列{an}的前n项积为，则，所以，所以答案选B

考查方向

本题主要考查了等比数列的性质

解题思路

利用等比数列的性质求出，进而求出Tn

易错点

1、忽略各项均为正数的条件；2、等比数列的性质

知识点

等比数列的基本运算等比数列的性质及应用

1

题型：单选题

|

单选题 · 5 分

4．在数列中，“对任意的，”是“数列为等比数列”的（）

A充分而不必要条件

B必要而不充分条件

C充分必要条件

D既不充分也不必要条件

正确答案

B

解析

当数列的通项为时，满足，但数列不是等比数列，即“对任意的，”不是“数列为等比数列”的充分条件；当数列为等比数列时，由等比中项得到，即“对任意的，”是“数列为等比数列”的必要条件，即“对任意的，”是“数列为等比数列”的必要不充分条件；所以选B选项。

考查方向

本题主要考查了充分条件、必要条件的判定，在近几年各省的高考题中出现的频率较高，常与函数的单调性、奇偶性、不等式的性质或解集、立体几何、解析几何、数列、概率等知识交汇命题．

解题思路

1．举特例（），说明即“对任意的，”不是“数列为等比数列”的充分条件；

2．再由等比中项，判定“对任意的，”是“数列为等比数列”的必要条件；

3．下结论。

易错点

本题易在判定是否为充分条件时出现错误，易忽视”数列为常数列0“的情形。

知识点

充要条件的判定等比数列的基本运算

1

题型：单选题

|

单选题 · 5 分

A

B

C

D

正确答案

B

知识点

等比数列的基本运算

1

题型：单选题

|

单选题 · 5 分

4．已知递减的等比数列满足，则（）

A63

B

C

D

正确答案

C

解析

解析已在路上飞奔，马上就到！

易错点

本题易运算上出错和审题上（忽略递减）导致导致出错。

知识点

等比数列的基本运算等比数列的性质及应用

1

题型：单选题

|

单选题 · 5 分

4,等比数列｛an｝满足a1=3， =21，则 ( )

A21

B42

C63

D84

正确答案

B

知识点

等比数列的基本运算

热门试卷

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

知识点

正确答案

解析

易错点

知识点

正确答案

知识点