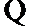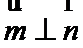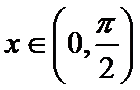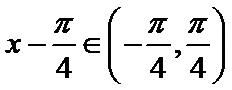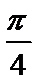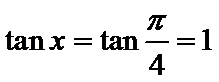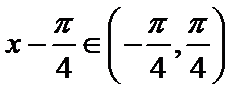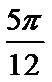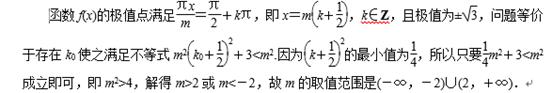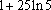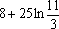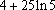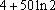- 三角函数的图象与性质
- 共712题
请考生从2题中选做一题
14.(坐标系与参数方程选做题)已知直线





15.(几何证明选讲选作题)如图1,已知












正确答案

解析
依题已知直线








考查方向
解题思路
先将直线
易错点
极坐标与平面直角坐标的互化。
正确答案

解析
如下图所示,连接












考查方向
解题思路
连接OC,则易得

易错点
图形中几何关系的寻找,射影定理的应用。
在平面直角坐标系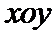
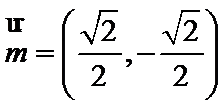
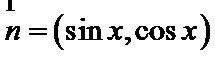
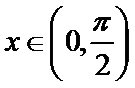
16.若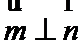
17.(2)若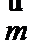
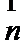
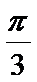
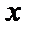
正确答案
(1)
解析
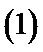
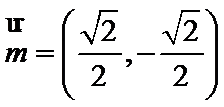
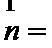
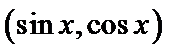
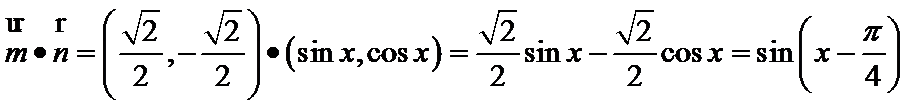
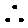
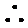

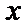

考查方向
解题思路
第一问,由两向量垂直,利用数量积等于零,结合坐标运算,可以得出正切值。
易错点
求解过程中注意角的范围,避免出现错解、多解现象
正确答案
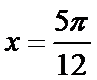
解析
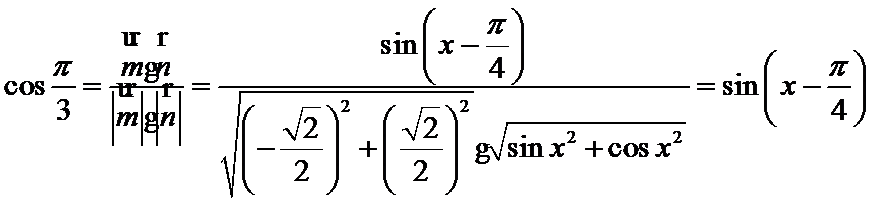

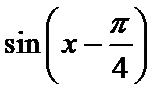
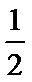

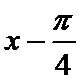
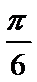

考查方向
解题思路
第二问,结合向量的夹角公式,列出方程求解即可。
易错点
求解过程中注意角的范围,避免出现错解、多解现象
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
设函数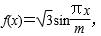
正确答案
解析
知识点
已知函数
(1) 当m=0时,求

(2) 当

正确答案
(1)
(2)m=-2
解析
(1)当m=0时,


从而得:
(2)
化简得:
当


代入上式,m=-2.
知识点
一辆汽车在高速公路上行驶,由于遇到紧急情况而刹车,以速度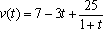
正确答案
解析
略
知识点
函数
正确答案
解析
f(x)=sinx-cos(x+





知识点
由曲线


正确答案
解析
用定积分求解
知识点
扫码查看完整答案与解析