三角函数的图象与性质
共712题

三角函数的图象与性质
共712题

热门试卷

X 查看更多试卷

题型：填空题

填空题 · 5 分

15.已知，且在区间有最小值，无最大值，则＝_______．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

三角函数的化简求值正弦函数的定义域和值域

题型：简答题

简答题 · 12 分

22．已知，定义域为D．

（1）化简，并求定义域D；

（2）是否存在，使得与相等？若存在，求的值；若不存在，请说明理由．

正确答案

（1），

，

又因为，

即，

解得：定义域为且．

（2）若，则，

所以，即，

此时，，

即为存在的值．

解析

解析已在路上飞奔，马上就到！

知识点

正弦函数的定义域和值域三角函数中的恒等变换应用

题型：单选题

单选题 · 5 分

6.函数的值域是（）

A[－4，0]

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

正弦函数的定义域和值域三角函数中的恒等变换应用三角函数的和差化积公式

题型：简答题

简答题 · 12 分

18.在中，三个内角，，的对边分别为，，，其中，且

（1）求证：是直角三角形；

（2）设圆过三点，点位于劣弧上，，用的三角函数表示三角形的面积，并求面积最大值.

正确答案

（1）证明：由正弦定理得，整理为，

即sin2A＝sin2B ∴2A＝2B或2A＋2B＝π,

即A＝B或A＋B＝∵，∴A＝B舍去.

由A＋B＝可知c＝，∴ΔABC是直角三角形

（2）由（1）及，得，

在RtΔ中，

所以，

，

因为，所以，，

当，即　时，最大值等于

解析

解析已在路上飞奔，马上就到！

知识点

正弦函数的定义域和值域两角和与差的正弦函数正弦定理

题型：填空题

填空题 · 4 分

11．函数的值域为（）

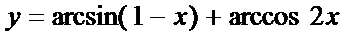
正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的值域反函数正弦函数的定义域和值域余弦函数的定义域和值域

题型：简答题

简答题 · 18 分

22．已知函数满足关系，其中是常数

（1）设，，求的解析式；

（2）设计一个函数及一个的值，使得；

（3）分别为的三个内角对应的边长，，若，且时取得最大值，求当取得最大值时的取值范围

正确答案

（1），；

（2），

若，则

，

（3）

因为且时取得最大值，

且

因为为三角形内角，所以，所以．

由正弦定理得，，

，，

所以的取值范围为

解析

解析已在路上飞奔，马上就到！

知识点

正弦函数的定义域和值域

题型：填空题

填空题 · 5 分

14.已知ΔABC中,∠A,∠B,∠C的对边分别为a,b,c,若a = 1, 2cosC + c = 2b,则ΔABC的周长的取值范围是__________.

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

正弦函数的定义域和值域

题型：简答题

简答题 · 10 分

17. 已知函数f（x）=cosx•sin（x+）﹣cos2x+，x∈R．

（1）求f（x）的最小正周期；

（2）求f（x）在闭区间[﹣，]上的最大值和最小值．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

三角函数的周期性及其求法正弦函数的定义域和值域三角函数中的恒等变换应用

题型：简答题

简答题 · 12 分

16．已知函数

（1）若函数的图象关于点对称，且，求t的值；

（2）设若p是q的充分条件，求实数m的取值范围。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

充要条件的应用正弦函数的定义域和值域正弦函数的对称性三角函数中的恒等变换应用

题型：简答题

简答题 · 12 分

17．已知函数f（x）＝cos（2x－）＋sin2x－cos2x．

（Ⅰ）求函数f（x）的最小正周期及其图象的对称轴方程；

（Ⅱ）设函数g（x）＝[f（x）] 2＋f（x），求g（x）的值域．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

二次函数在闭区间上的最值三角函数的周期性及其求法正弦函数的定义域和值域正弦函数的对称性三角函数中的恒等变换应用

继续学习学习下一知识点

下一知识点 : 三角恒等变换

百度题库 > 高考 > 理科数学 > 三角函数的图象与性质

扫码查看完整答案与解析