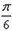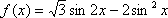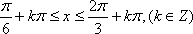- 三角函数的图象与性质
- 共712题
如图,已知四棱锥P—ABCD,底面ABCD为矩形,

(1)求异面直线PB与AC所成的角的余弦值;
(2)求

正确答案
见解析
解析
(1



设





(2)
知识点
在

正确答案
解析
略
知识点
已知


正确答案
1
解析
略
知识点

正确答案
解析



知识点
在△ABC中,角A,B,C所对的边分别为a,b,c,且满足
(1)求角C的大小;
(2)求
正确答案
见解析。
解析
(1)由csinA=



∴sinC=

∵0<C<π,∴C=
(2)由(1)知B=
∴




=





∵0<A<



当A+





知识点
已知 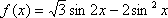
(1)求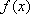
(2)若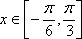
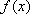

正确答案
(1)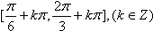
解析
(1)因为
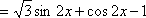
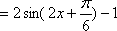
所以,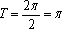
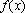

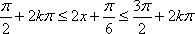
所以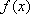
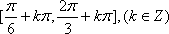
(2)因为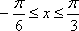
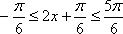
所以有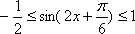
由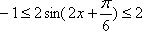
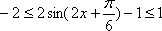
所以,函数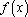
此时,因为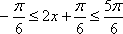
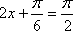
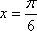
知识点
锐角△ABC中,角A,B,C所对的边分别为a,b,c,已知sinA=
(1)求cosA的值并由此求
(2)若a=6,
正确答案
见解析。
解析
(1)因为锐角△ABC中,A+B+C=,

………………………………………………………………………………………………….6分
(2)
则


由余弦定理:


知识点
函数y=sinx+sin(x﹣
正确答案
2π;
解析
解:因为函数y=sinx+sin(x﹣




所以函数的周期为T=
函数的最大值为:
知识点
设函数



(1)求
(2)在








正确答案
见解析
解析
(1)

令

(2)由


∵
又∵

∴在

由

知识点
设函数



(1)求
(2)在








正确答案
见解析
解析
(1)

令

(2)由


∵
又∵

∴在

由

知识点
扫码查看完整答案与解析