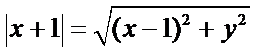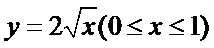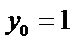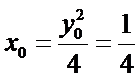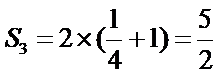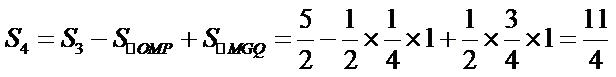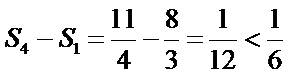- 三角函数的图象与性质
- 共712题
在
15.求
16.求
正确答案
（1）
解析
（1）根据余弦定理公式求出cosB的值，进而根据B的取值范围求B的大小；
考查方向
解题思路
正、余弦定理是应用极为广泛的两个定理，它将三角形的边和角有机地联系起来，从而使三角与几何产生联系，为求与三角形有关的量提供了理论依据，也是判断三角形形状、证明三角形中有关等式的重要依据．注意体会其中蕴涵的函数与方程思想、等价转化思想及分类讨论思想．
易错点
1)正余弦定理，
2)三角恒等变形公式
正确答案
（2）
解析
考查方向
解题思路
正、余弦定理是应用极为广泛的两个定理，它将三角形的边和角有机地联系起来，从而使三角与几何产生联系，为求与三角形有关的量提供了理论依据，也是判断三角形形状、证明三角形中有关等式的重要依据．注意体会其中蕴涵的函数与方程思想、等价转化思想及分类讨论思想．
易错点
1)正余弦定理，
2)三角恒等变形公式
有一块正方形菜地
21.求菜地内的分界线
22.菜农从蔬菜运量估计出
正确答案
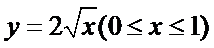
解析
设分界线上任一点为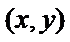
可得
考查方向
解题思路
根据抛物线定义或者直接列式得到曲线方程；
正确答案
矩形面积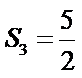
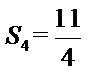
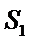
解析
设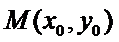
∴
∴设所表述的矩形面积为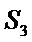
过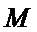
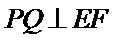
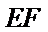
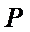
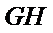
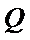
设五边形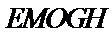
∵
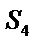
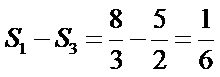
∴五边形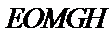
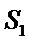
考查方向
解题思路
分别求得矩形和五边形的面积，然后求得其与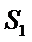
易错点
对“更接近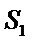
6.已知
A
B
C
D
正确答案
知识点
设f（x）=sinxcosx﹣cos2（x+
16.求f（x）的单调区间；
17.在锐角△ABC中，角A，B，C的对边分别为a，b，c，若f（
正确答案
单调递减区间是
解析
（Ⅰ）由题意
由
可得
由
得
所以
单调递减区间是
考查方向
解题思路
（Ⅰ）由三角函数恒等变换化简解析式可得f（x）
易错点
两角和与差的正弦函数的化简变换，正弦函数的单调性的整体变换
正确答案
解析
（II）
由题意A是锐角，所以 
由余弦定理：
考查方向
解题思路
【解题思路】（Ⅱ）由
易错点
余弦定理的变形，基本不等式的应用．
当今全球规模最大的单一金融市场和投机市场是_________。
A．股票市场
B．黄金市场
C．期货市场
D．外汇市场
正确答案
D
解析
暂无解析
已知函数
15.求
16.若将
求函数
正确答案
详见解析
解析
解 (1)
考查方向
函数y=Asin（ωx+φ）的图象变换；三角函数的周期性及其求法．
解题思路
利用倍角公式及诱导公式化简，然后由周期公式求周期
易错点
计算化简能力弱，三角函数性质掌握不牢固
正确答案
详见解析
解析
(2)由已知得
故当
当
考查方向
函数y=Asin（ωx+φ）的图象变换；三角函数的周期性及其求法．
解题思路
由三角函数的图象平移得到函数g（x）的解析式，结合x的范围求得函数g（x）在区间
易错点
计算化简能力弱，三角函数性质掌握不牢固
请你谈一谈对“不同生产方式以及生产工艺中，生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
为了得到函数
A向左平移
B向右平移
C向左平移
D向右平移
正确答案
解析
略
知识点
对于函数f(x)=2sinxcosx，下列选项中正确的是 【】
Af(x)在（
Bf(x)的图象关于原点对称
Cf(x)的最小正周期为
Df(x)的最大值为2
正确答案
解析
本题考查三角函数的性质
f (x)=2sinxcosx=sin2x，周期为π的奇函数
知识点
3.如图，某港口一天6时到18时的水深变化曲线近似满足函数
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
扫码查看完整答案与解析