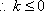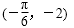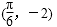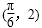- 三角函数的图象与性质
- 共712题
在△ABC中,内角A、B、C的对边长分别为a,b,c,已知

正确答案
4
解析
略
知识点
已知函数

(1)求

(2)求函数

正确答案
(1)1;
(2)
解析

(1)
显然,函数

(2)令


又因为

函数


知识点
如图2,在矩形

围成的区域为

点


正确答案
解析
略
知识点
对于函数
正确答案
解析
略
知识点
已知定点

(1)求曲线E的方程;
(2)若点A的坐标为

正确答案
见解析。
解析
(1)由题意, 点


故点


∴曲线

(2)设点


由


∴
直线

故直线

令

∴点

同理可得点

∴

∴
设线段

则

∴以线段

展开得
令



∴以线段

知识点
函数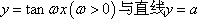
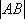
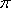
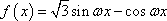
正确答案
解析
略
知识点
已知向量
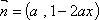
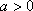

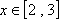
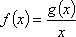
(1)求实数
(2)若不等式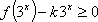
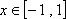
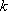
正确答案
(1)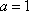
解析
(1)由题得
又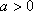
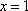
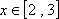
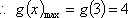
(2)由(1)的他,
令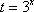
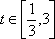
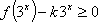
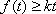
即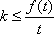
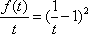

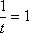
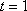
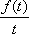
知识点
已知函数
(1)求
(2)求

正确答案
(1)
(2)
解析
(1)


∴函数

由 

得 
∴


(2)





知识点
已知函数

(1)求函数
(2)已知







正确答案
见解析。
解析
(1)



由





(2)∵


∵


即

由余弦定理

即

∴
知识点
8.函数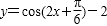
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析