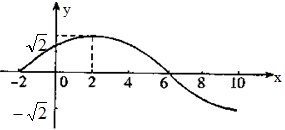
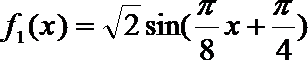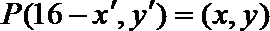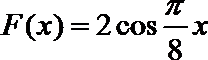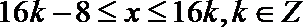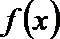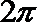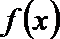三角函数的图象与性质
共712题

三角函数的图象与性质
共712题

热门试卷

X 查看更多试卷

题型：单选题

单选题 · 5 分

2．ω是正实数，函数在上是增函数，那么（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

正弦函数的单调性

题型：简答题

简答题 · 12 分

20. 已知双曲线C的两条渐近线过坐标原点，且与以点为圆心，1为半径的圆相切，双曲线C的一个顶点与点A关于直线对称，设直线过点A，斜率为

（1）求双曲线的方程；

（2）当时，在双曲线C上支求点B，使其与直线的距离为

（3）当时，若双曲线C的上支上有且只有一个点B到直线的距离为，求斜率的值及相应点B的坐标。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

正弦函数的单调性

题型：简答题

简答题 · 12 分

18 ．已知函数

（1）求函数的对称中心和单调区间；

（2）已知内角的对边分别为，且，若向量与共线，求的值。

正确答案

（1）原式整理得，

对称中心为，单调增区间为

单调减区间为

（2）∵，∴，

∴C＝

∵与共线，

及由正弦定理得

由余弦定理得，

∴

解析

解析已在路上飞奔，马上就到！

知识点

正弦函数的单调性正弦函数的对称性三角函数中的恒等变换应用解三角形的实际应用平面向量共线（平行）的坐标表示

题型：单选题

单选题 · 5 分

8．设函数的图像关于直线对称,它的周期是,则（）

A的图象过点

B的一个对称中心是

C在上是减函数

D将的图象向右平移个单位得到函数的图象

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

三角函数的周期性及其求法正弦函数的单调性正弦函数的对称性函数y=Asin（ωx+φ）的图象变换

题型：简答题

简答题 · 13 分

17．已知函数的部分图象如图所示：

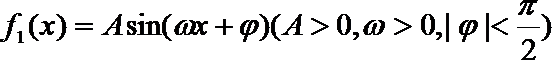
（1）求此函数的解析式；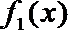

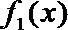
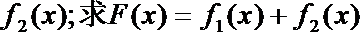
（2）与的图象关于x=8对称的函数解析式单增区间。

正确答案

（1）

（2）设上，则P′点关于x=8对称点

，

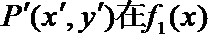
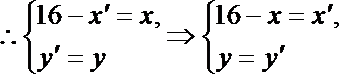
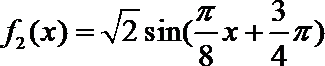
单增区间

解析

解析已在路上飞奔，马上就到！

知识点

函数的图象与图象变化正弦函数的单调性由y=Asin（ωx+φ）的部分图象确定其解析式三角函数中的恒等变换应用

题型：简答题

简答题 · 13 分

18. 已知函数.

（Ⅰ）求函数的周期及的最大值和最小值；

（Ⅱ）求在上的单调递增区间。

正确答案

解：（Ⅰ）

（Ⅱ）的单调递增区间为

所以，上的单调递增区间为

解析

解析已在路上飞奔，马上就到！

知识点

三角函数的周期性及其求法正弦函数的单调性三角函数中的恒等变换应用三角函数的最值

题型：简答题

简答题 · 12 分

16．已知函数，三个内角的对边分别为．

（I）求的单调递增区间及对称轴的方程；

（Ⅱ）若，求角的大小．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

正弦函数的单调性正弦函数的对称性三角函数中的恒等变换应用余弦定理

题型：单选题

单选题 · 5 分

5．已知函数，则（）

A函数的周期为

B函数在区间上单调递增

C函数的图象关于直线对称

D函数的图象关于点对称

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

三角函数的周期性及其求法正弦函数的单调性正弦函数的对称性三角函数中的恒等变换应用

题型：简答题

简答题 · 12 分

18．已知函数的最小正周期为

（1）求的单调递增区间；

（2）在中，、、分别是角A、B、C的对边，若的面积为，求实数的值。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

正弦函数的单调性三角函数中的恒等变换应用正弦定理

题型：简答题

简答题 · 12 分

17．已知函数的图像经过点A（0，1）、。

（1）当时，求函数的单调增区间；

（2）已知，且的最大值为，求的值。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

正弦函数的单调性三角函数中的恒等变换应用三角函数的最值

继续学习学习下一知识点

下一知识点 : 三角恒等变换

百度题库 > 高考 > 理科数学 > 三角函数的图象与性质

扫码查看完整答案与解析