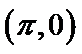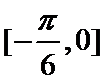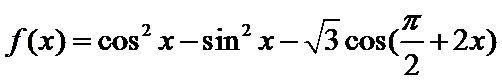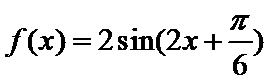- 三角函数的图象与性质
- 共712题
1.已知函数f(x)=sin(2ωx+



正确答案
解析
因为f(x)相邻两条对称轴之间的距离为


又T=


将f(x)的图象向右平移
f(x)=sin[4(x-



令2x-



若g(x)+k=0在x∈[0,
即y=sin t与y=-k在[-

如图所示,由正弦函数的图象可知-



知识点
20.把函




(1)求a的最小值;
(2)当a取最小值,求函数

正确答案
(1)
∴

∴


(2)由(1)知
即
解析
解析已在路上飞奔,马上就到!
知识点
5.已知函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.设函数









正确答案
解析
在
若
则

∴

∴
∴
故选C.
考查方向
本题考查函数的性质,考查即时学习能力,是中档题.新定义的学习型问题,在近几年各省市高考中出现的频率很高,常以压轴题的形式出现,整合函数、数列、解析几何、三角、向量等知识,体现数学多种思想方法.
解题思路
先求


易错点
对新定义对称中心的不理解.
知识点
7.定义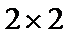
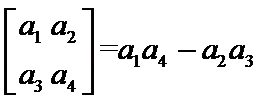
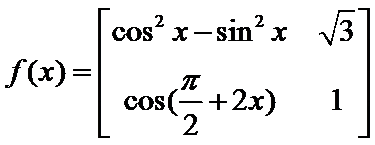
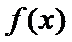
正确答案
解析
根据矩阵的定义,可以得到
所以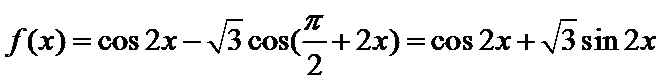
根据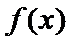
考查方向
三角函数
解题思路
先根据矩阵的定义,得到f(x)的解析式,然后根据函数的解析式判断函数的相关性质.
易错点
三角函数公式记忆混淆
知识点
4.已知函数




正确答案
解析
由题意得













考查方向
本题主要考查三角函数的图像和性质、诱导公式等知识,意在考查考生对于三角函数基础知识的掌握程度。
解题思路
1.先根据题中条件求出函数
2.然后利用对称中心的坐标公式求出此函数的对称中心。
易错点
1.图像平移时容易错写成
2.混淆对称中心与对称轴导致结果出错。
知识点
6.若函数

正确答案
解析
将

得到
得到
又因为
所以
求对称轴,
解得
考查方向
解题思路
将


易错点
1、正弦值为

2、忽略题中给出的、忽略题中给出的
知识点
8.设函数


正确答案
解析
由题得周期为




考查方向
解题思路
该题首先根据周期求出

易错点
本题易错在(1)忽略A为负值(2)对称中心计算错误(3)单调性不能判断
知识点
(4分)(2015•上海)已知函数f(x)=sinx.若存在x1,x2,…,xm满足0≤x1<x2<…<xm≤6π,且|f(x1)﹣f(x2)|+|f(x2)﹣f(x3)|+…+|f(xm﹣1)﹣f(xm)|=12(m≥12,m∈N*),则m的最小值为 .
正确答案
8
知识点
8.已知




正确答案
解析
三角函数相邻两对称轴正好跨度了半个周期所以



又

考查方向
解题思路
利用堆成轴间距求出周期确定
易错点
无法利用条件确定周期进而求解
知识点
扫码查看完整答案与解析