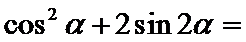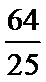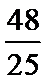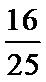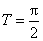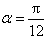- 三角函数的图象与性质
- 共712题
5.若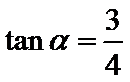
正确答案
解析
由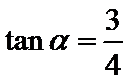
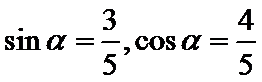
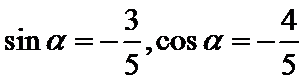
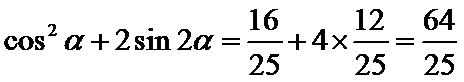
考查方向
解题思路
由正切值求正弦余弦,然后结合倍角公式求值。
易错点
三角函数值的符号问题,三角公式的应用
知识点
6.已知函数




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.当

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.已知锐角A,B满足tan(A+B)=2tanA,则tanB的最大值是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
已知


正确答案
-
解析
略
知识点
函数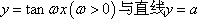
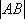
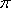
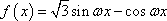
正确答案
解析
略
知识点
已知函数
(1) 试说明函数

(2) (理科)若函数



(3) 求函数
正确答案
见解析
解析
(1)∵

∴
∴函数

①将函数


②将函数


③将函数

(说明:横坐标先放缩,再平移也可,即将函数







(2)由(1)知,
∴
又对任意

∴函数
∵
∴

现用反证法证明

反证法:假设



则

令




所以,函数

(3)先求函数

当


易知,此时函数


函数的取值范围是
因此,依据周期函数的性质,可知函数


函数

知识点
已知函数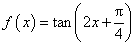
(1)求函数的定义域与最小正周期;
(2)设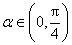
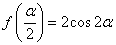
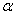
正确答案
(1)最小正周期为
(2)
解析
(1)函数的定义域满足
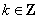
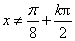
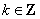
所以函数的定义域为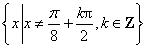
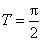
(2)解法1。 因为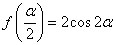
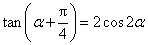
所以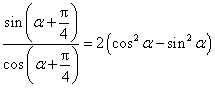
于是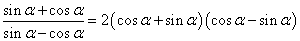
因为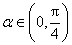
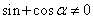
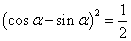
因而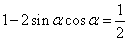
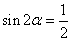
因为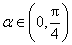
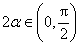
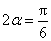
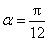
解法2。因为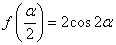
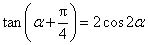
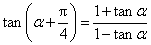
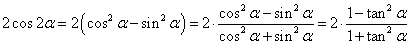
所以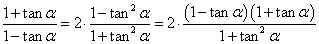
因为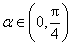
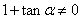
于是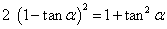
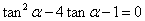
所以
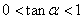
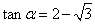
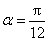
解法3。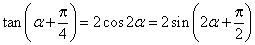

因为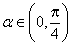
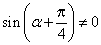
得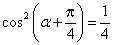
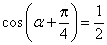
于是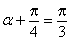
知识点
已知命题





正确答案
解析
略
知识点
9. 函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析