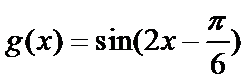- 三角函数的图象与性质
- 共712题
4.要得到函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7. 已知函数





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.将函数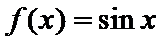
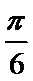
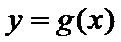
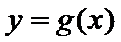
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6. 函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.已知函数f(x)=sin(2ωx+



正确答案
解析
因为f(x)相邻两条对称轴之间的距离为


又T=


将f(x)的图象向右平移
f(x)=sin[4(x-



令2x-



若g(x)+k=0在x∈[0,
即y=sin t与y=-k在[-

如图所示,由正弦函数的图象可知-



知识点
20.把函




(1)求a的最小值;
(2)当a取最小值,求函数

正确答案
(1)
∴

∴


(2)由(1)知
即
解析
解析已在路上飞奔,马上就到!
知识点
5.已知函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.已知向量

(1)求出

(2)

(3)设



正确答案
(1)
其振幅为

(2)可由



(3)由
∵ 


∴
解析
解析已在路上飞奔,马上就到!
知识点
26.已知函数





正确答案


解析
试题分析:
本题属于三角函数中的基本问题,题目的难度是逐渐由易到难,
(1)直接按照步骤来求
(2)要注意公式的应用
由


再把横坐标缩短到原的

由
所以
考查方向
本题考查了三角函数图像变换的知识,涉及到图像性质,是高考题中的高频考点
解题思路
本题考查三角函数图像变换,解题步骤如下:
1、利用伸缩平移变换化简。
2、利用公式代入求解。
易错点
平移变换时容易出错。
知识点
扫码查看完整答案与解析