- 函数的基本性质
- 共1843题
设函数
(1)求f(x)的值;
(2)设函数
(3)设a>0,试讨论方程
正确答案
见解析
解析
解析:(1)
令f’(x)=0得x
由上表知当

(2)由g(x)≤x+m≤f(x)在(0,+∞)上恒成立得
由



∵当x→0时,
当0<a<e时,
当a=e时,
当a>e时,
知识点
设


正确答案
解析
∵


∴
∵
∴
知识点
复数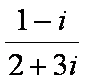
正确答案
解析
解:可化为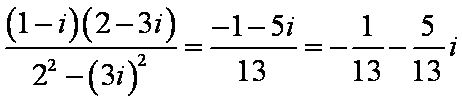
知识点
已知函数
(1)求函数
(2)若




正确答案
见解析。
解析
(1)令

由此可得所求函数的定义域为
(2)当


取等条件是


原不等式等价于

又
当




知识点
某品牌电视机代理销售商根据近年销售和利润情况得出某种型号电视机的利润情况有如下规律:每台电视机的最终销售利润


设每台该种电视机的无故障使用时间







(1)求


(2)记

正确答案
见解析
解析
(1)∵


解得

(2)X的取值有0,100,200,300,400,





所以
数学期望
知识点
在平面直角坐标系








(1)求直线
(2)试判断直线




正确答案
见解析
解析
解析:
(1)由直线


所以直线
当




所以直线
(2)直线





又点P到直线



设直线






知识点
某几何体的三视图如图所示,则它的表面积为
正确答案
解析
由几何体的三视图可知,该几何体是一个沿旋转轴作截面,截取的半个圆锥,底面半径是1,高是2,所以母线长为

知识点
某高校在2011年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组:第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100]得到的频率分布直方图如图所示。
(1)分别求第3,4,5组的频率;
(2)若该校决定在笔试成绩高的第3,4,5组中用分层抽样抽取6名学生进入第二轮面试,
正确答案
解析
(1)第三组的频率为0.06
第四组的频率为0.04
第四组的频率为0.02
(2)(A)设M:学生甲和学生乙同时进入第二轮面试
P(M)=

(B)

知识点
在平面直角坐标系






(1)求
(2)在以






正确答案
见解析
解析
解(1)直线


代入曲线
设



所以
(2)由极坐标与直角坐标互化公式得

所以点

中点

由参数




知识点
设函数




正确答案
解析
由
















知识点
扫码查看完整答案与解析






























