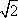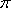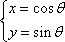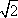- 直线与圆相交的性质
- 共47题
如图,已知



正确答案
解析
略
知识点
在极坐标系中,圆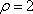
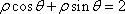
正确答案
解析
略
知识点
在极坐标系中,直线

正确答案
解析
略
知识点
动圆C经过点F(1,0),并且与直线x=-1相切,若动圆C与直线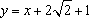
正确答案
解析
略
知识点
在平面直角坐标系中,已知直线C
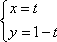


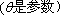
正确答案
解析
略
知识点
已知极坐标系与直角坐标系长度单位相同,且以原点O为极点, x轴的非负半轴为极轴. 设直线C1: 
(1) 当

(2)求曲线C1与C2两交点的直角坐标(用
正确答案
见解析
解析
(1)当

又因为
故曲线C1的极坐标方程为

当


(2)消去参数得C1的普通方程为

二者联立,将
得
因为判别式△=4,所以设其二根分别为

即所求的中点的直角坐标为(

知识点
已知直线


(1)设



(2)若把曲线






正确答案
见解析
解析
(1)

联立方程组





(2)



从而点


由此当


知识点
在直角坐标系




(1)求圆
(2)直线







正确答案
见解析
解析
(1)圆

所以圆

(2)设

设

所以
知识点
在直角坐标系


(



程是
(1)将圆
(2)若直线



正确答案
见解析
解析
解:(1)∵
∴ 

∴圆

圆心的直角坐标为

(2)直线


代入圆

设


∴
知识点
10.已知直线ax+by+c=0与圆O:x2+y2=1相交于A、B两点,且|AB|=

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析