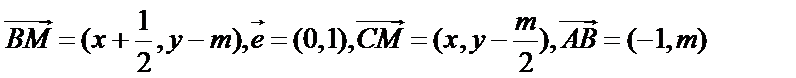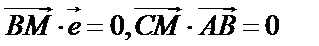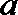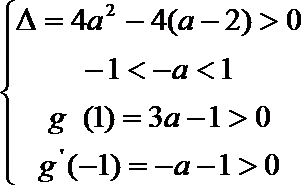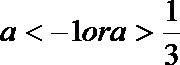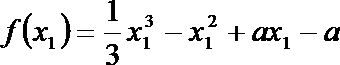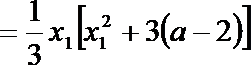- 换底公式的应用
- 共23题
17.在




(1)求角A的大小;
(2)若

正确答案
(1)

(2)∵
∴
即





解析
解析已在路上飞奔,马上就到!
知识点
22.对任意




(1)当


(2)求

(3)当


正确答案
(1)当


当


(2)
对任何



即
由(Ⅰ)的结论,

(3)解:
①当
②容易验证

③当
设
则
所以当


④当
设

所以方程没有
综上可知,若
解析
解析已在路上飞奔,马上就到!
知识点
12.已知函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.已知


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.
正确答案
-1
解析
解析已在路上飞奔,马上就到!
知识点
7.一个社会调查机构就某地居民的月收入调查20000人,并根据所得数据画出了样本频率分布直方图,为了分析居民的收入与年龄、学历、职业等方面的关系,按月收入用分层抽样方法抽样,若从月收入
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.在平面直角坐标系中,已知点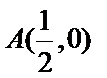
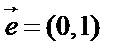
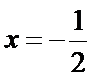

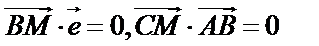
(1)试求动点M的轨迹E的方程;
(2)设点P是轨迹E上的动点,点R、N在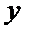
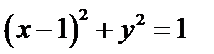
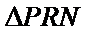
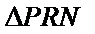
正确答案
(1)设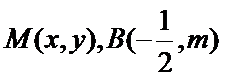
则
由
得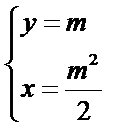
所以动点M的轨迹E的方程为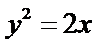
(2)设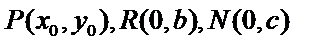
且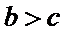
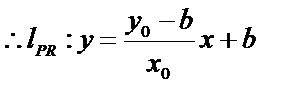
即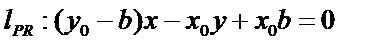
由相切得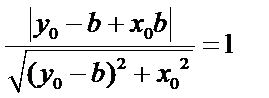
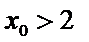
化简得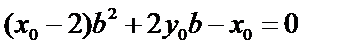
同理得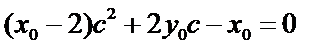
所以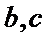
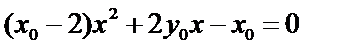
所以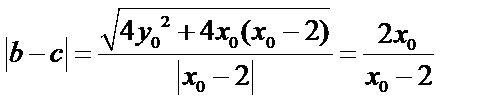
有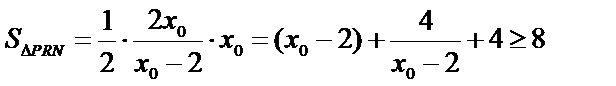
当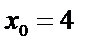
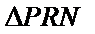
解析
解析已在路上飞奔,马上就到!
知识点
14.若


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
22. 已知函数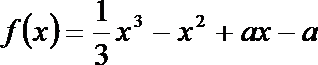
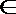
(1)当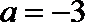
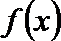
(2)设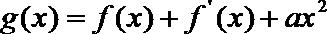
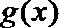
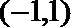
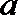
(3)若函数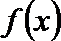
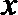
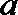
正确答案
解:(1)当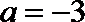
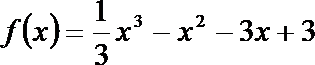
∴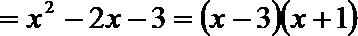
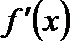
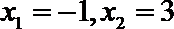
当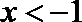
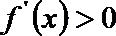
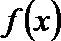
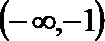
当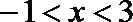
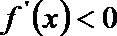
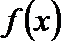
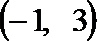
当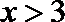
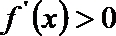
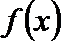
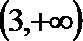
问题转化为方程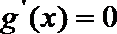
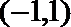
∴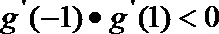
解得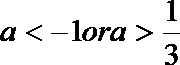
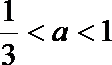
(3) ∵ 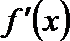
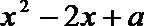
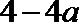
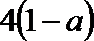
① 若a≥1,则△≤0, ∴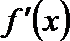
∴ f(x)在R上单调递增 .
∵f(0)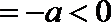
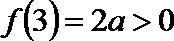
∴当a≥1时,函数f(x)的图象与x轴有且只有一个交点.
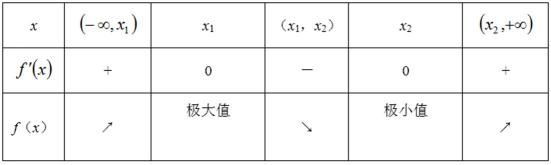
当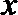
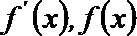
∵
∴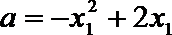
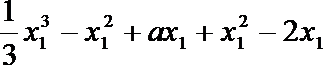
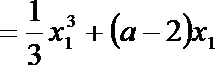
解析
解析已在路上飞奔,马上就到!
知识点
16.函数




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析